What is Data?
Data is information describing some phenomenon.
What is a Phenomenon?
A factor situation that is observed to exist or happen, especially one whose cause or explanation is in question.
- A lightning strike

What is a Phenomenon?
A factor situation that is observed to exist or happen, especially one whose cause or explanation is in question.
- A lightning strike
- A coastline

What is a Phenomenon?
A factor situation that is observed to exist or happen, especially one whose cause or explanation is in question.
- A lightning strike
- A coastline
- A country
What is a Phenomenon?
A factor situation that is observed to exist or happen, especially one whose cause or explanation is in question.
- A lightning strike
- A coastline
- A country
- A dog on a kayak!

Anything and everything are phenomena!
Types of Phenomena
Discrete Objects
Distinct boundaries
Chat can be exactly measured
Finite
They are countable and cannot be infinitely subdivided
Continuous Fields
No distinct boundaries
Everywhere has a value
Infinitely divisible
They are not countable and can be infinitely subdivided
Types of Phenomena
When is a phenomenon discrete or continuous?
- To an extent, it depends on our perspective and the scale of our analysis.
- Many phenomenon are a bit of both.
Lightning
A strike is a discrete object, what about a lighting bolt?
- Sort of continuous?

Lightning
A strike is a discrete object, what about a lighting bolt?
- Strike frequency is a continuous field
- Everywhere has a value
- Even the absence of strikes, is a frequency of strikes
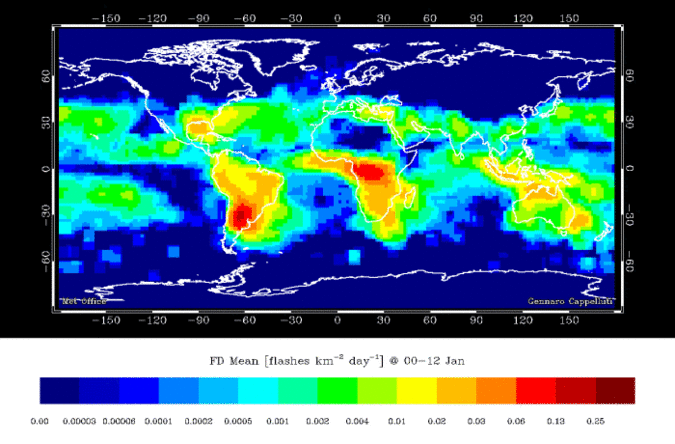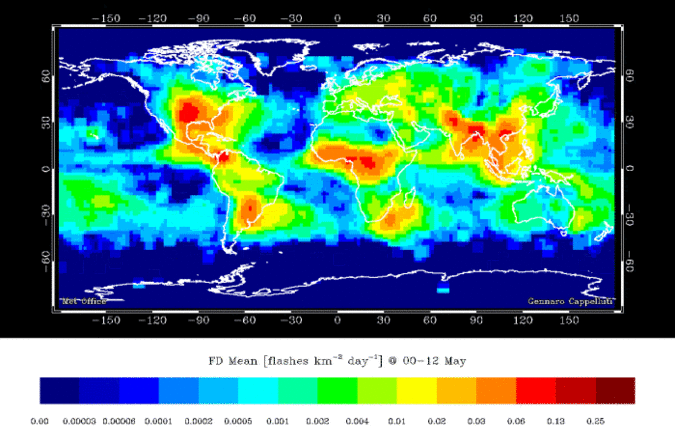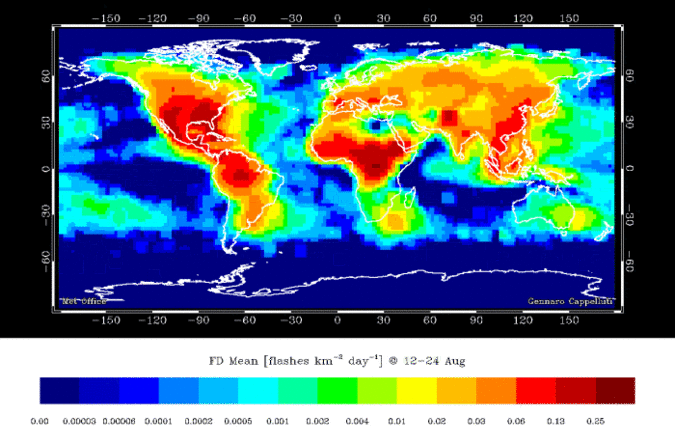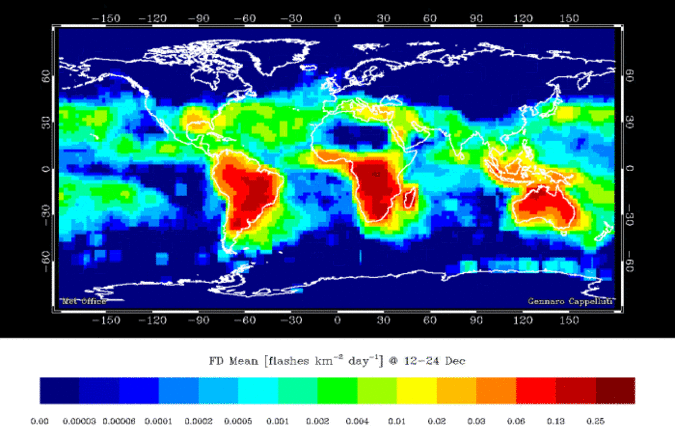
A Coastline
Continuous field at large scale
- Tides & waves
- Where is the exact boundary?

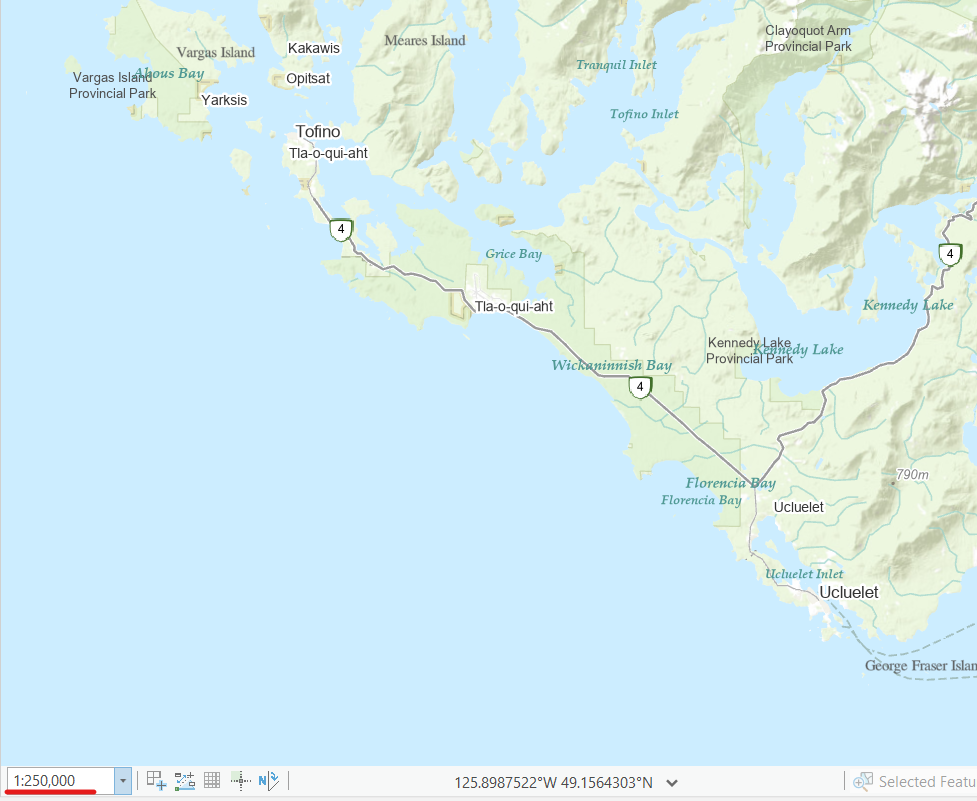
A Coastline
Discrete object at small scale
- Zoom out and the tides/waves don’t really matter
- Its easy to draw a static boundary
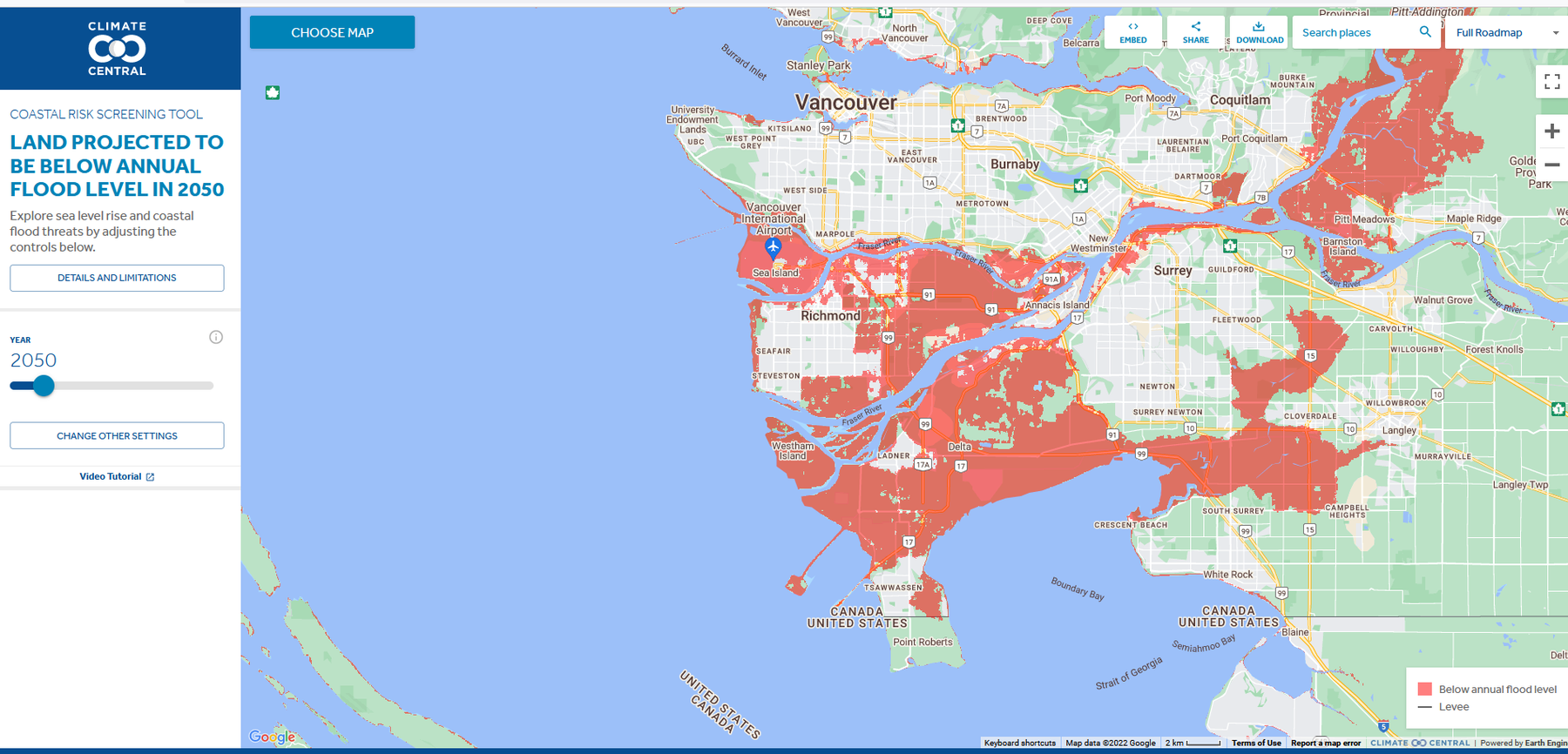
A Coastline
Unless you change the time scale
Types of Phenomena
Most things don’t fall perfectly into one category or the other.
- That said, it is a helpful framework as long as we recognize the discrete vs. continuous dichotomy is not a perfect classification
TopHat Question 1
Discrete objects: (select all that apply)
- Are countable
- Do not have distinct boundaries
- Are infinitely divisible
- Have well defined boundaries
Discrete Objects
Buildings are a great example.
- Concrete boundaries
- Countable
- Real physical object

Discrete Objects
Political Boundaries are also a great example.
- Distinct boundaries
- Countable
- Not a physical object

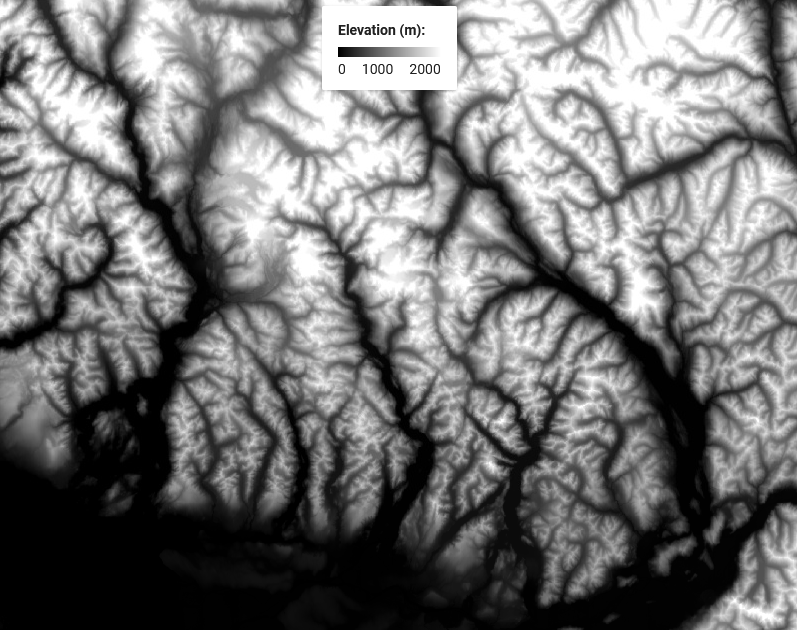
Continuous Fields
Elevation is a great example.
- Everywhere on Earth
- No “number of elevations”
- A physical property
Continuous Fields
Density of tweets is also a great example.
Everywhere has this too
Derived from something countable
But not countable itself
Not a physical property
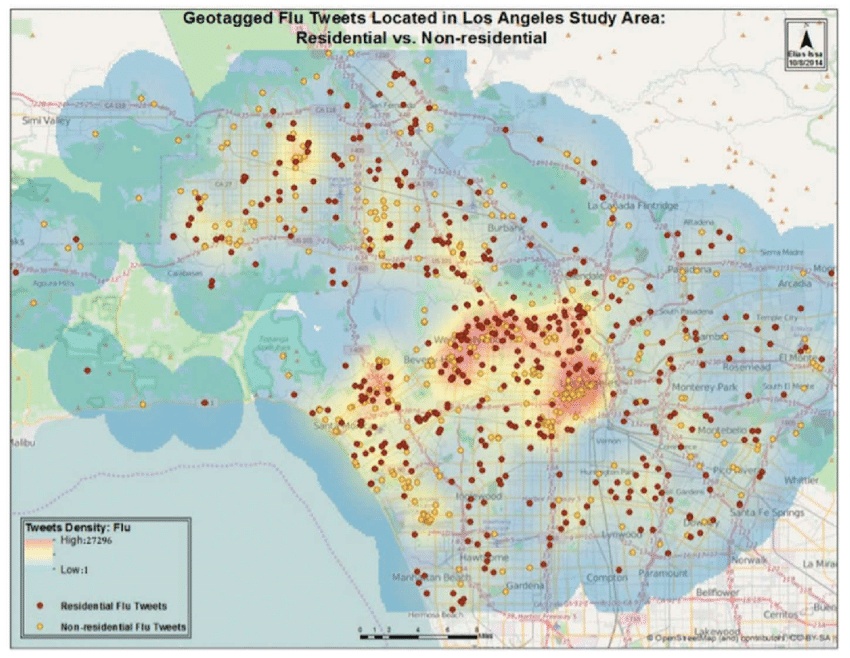
Working Together
Frequently we’ll end up working with both discrete objects and continuous fields.
- In Module 1, you worked with:
- Cholera deaths
- Discrete objects
- Kernel density
- Continuous field
- Cholera deaths
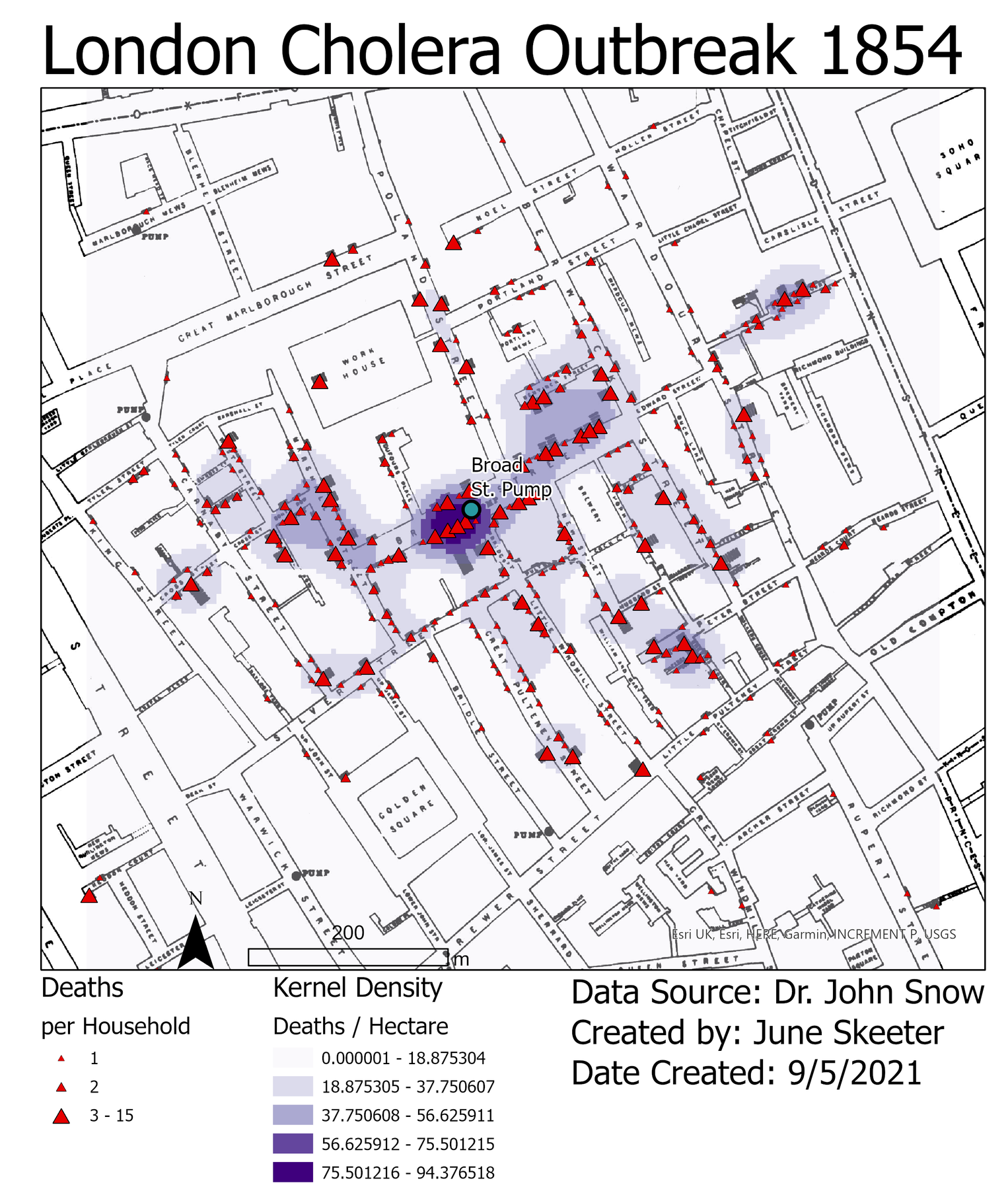
Digital information
We’ll talk more about spatial data models later. For now, lets think about data more broadly.
- How do we represent data in a computer?
Digital information
Digital information is represented as bits (0’s and 1’s)
- We typically quantify data as bytes (8 bits):
- Kilobyte (kB) = 1,000 bytes
- Megabyte (MB) = 1,000,000 bytes
- Gigabyte (GB) = 1,000,000,000 bytes
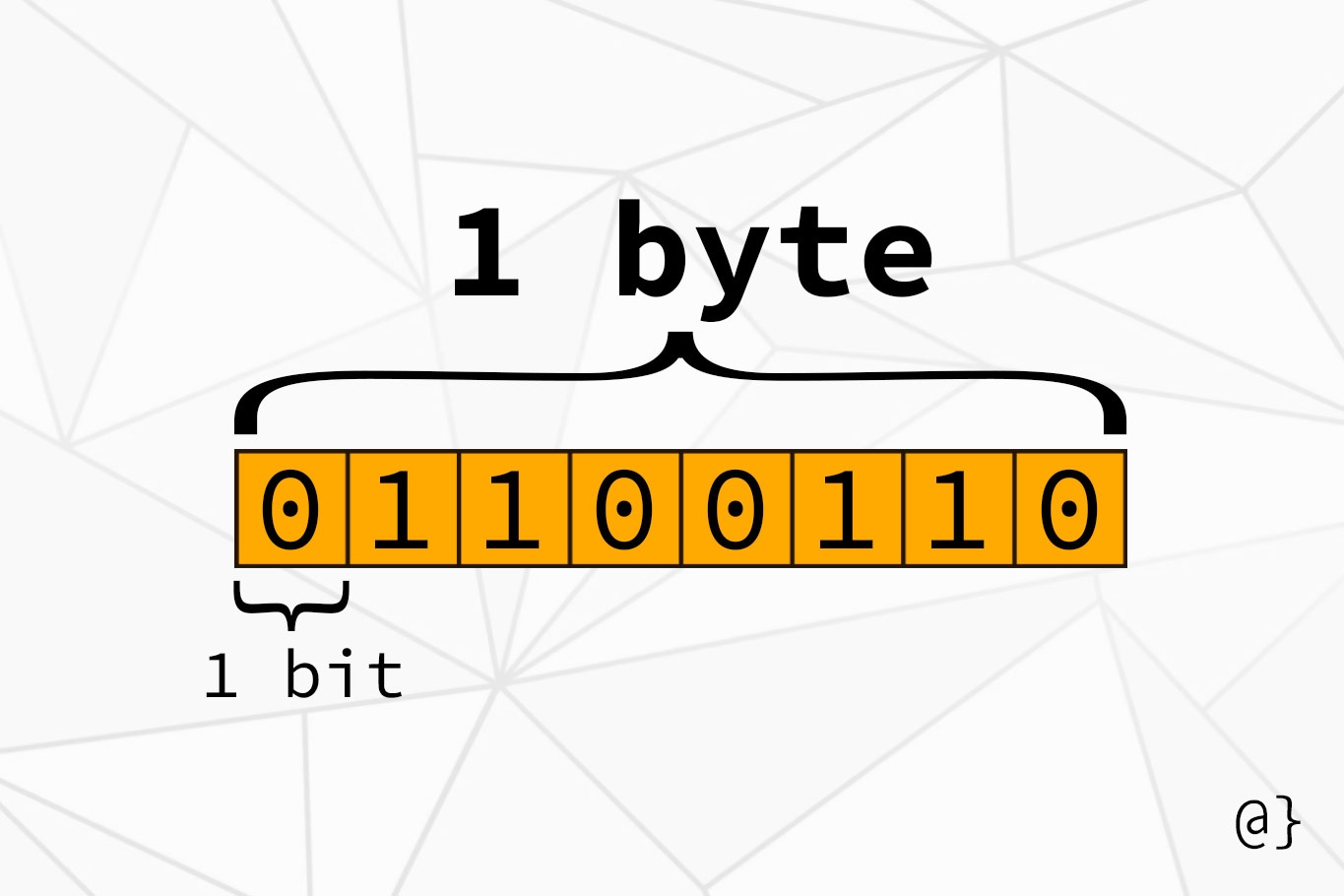
Digital information
There are numerous ways to translate human readable data to binary, such as ASCII.
- Each character is represented as one byte
- 28 = 256 unique combinations of 0’s and 1’s in a byte
- Some examples:
- “A” : 01000001
- “CAT”: 01000011 01000001 01010100
- “31”: 00110011 00110001
Digital Information
Modern computers use 64-bit “architecture”. The central processing unit (CPU) can handle 64 bits (8 bytes) of information at a time.
- “Word” length is 64 bits, a word is a unit of data
i.e., an individual piece of information
18 quintillion unique combinations of 1’s and 0’s
- CPUs can be stacked in parallel to handle more information at one time
Representing Phenomena in GIS
Within the context of a GIS, every piece of information describing a phenomenon is referred to as an Attribute.
- Broadly speaking each attribute can address one of three questions:
- Where?
- What?
- When?
Types of Attributes
There are multiple ways to classify/think about attributes. One important distinction we must make
- Non-Spatial Attributes: describe what or when
- Spatial Attributes: describe where
- Puts the Geographic in GIS
- Requires some special considerations
- We have already talked a bit about map projections
- We’ll discuss more considerations in the next module
Types of Attributes
All data (attributes), spatial and non-spatial, can be either qualitative or quantitative.
- Analysis we can do with qualitative data are more limited
- Does not make quantitative data “better”
- Measurement scales: both qualitative and quantitative can be measured on different scales
- Qualitative: Nominal or Ordinal Sales
- Quantitative: Interval or Ratio Sales
Qualitative Data
Qualitative data is Categorical. It is strictly descriptive and lacks any meaningful numeric value.
- Textual, coded numerals, pictures, sounds, etc
- Typically working with textual & coded numerals most frequently in GIS
- Limited number of computational options, often requires careful consideration when analyzing
- Measured on either a Nominal or Ordinal scale.
Nominal Scale
Names or categories with no ranking or direction. Categories are not more/less, better/worse, they just different. Some examples include:
- Flower Species

Nominal Scale
Names or categories with no ranking or direction. Categories are not more/less, better/worse, they just different. Some examples include:
- Flower Species
- Zoning Categories
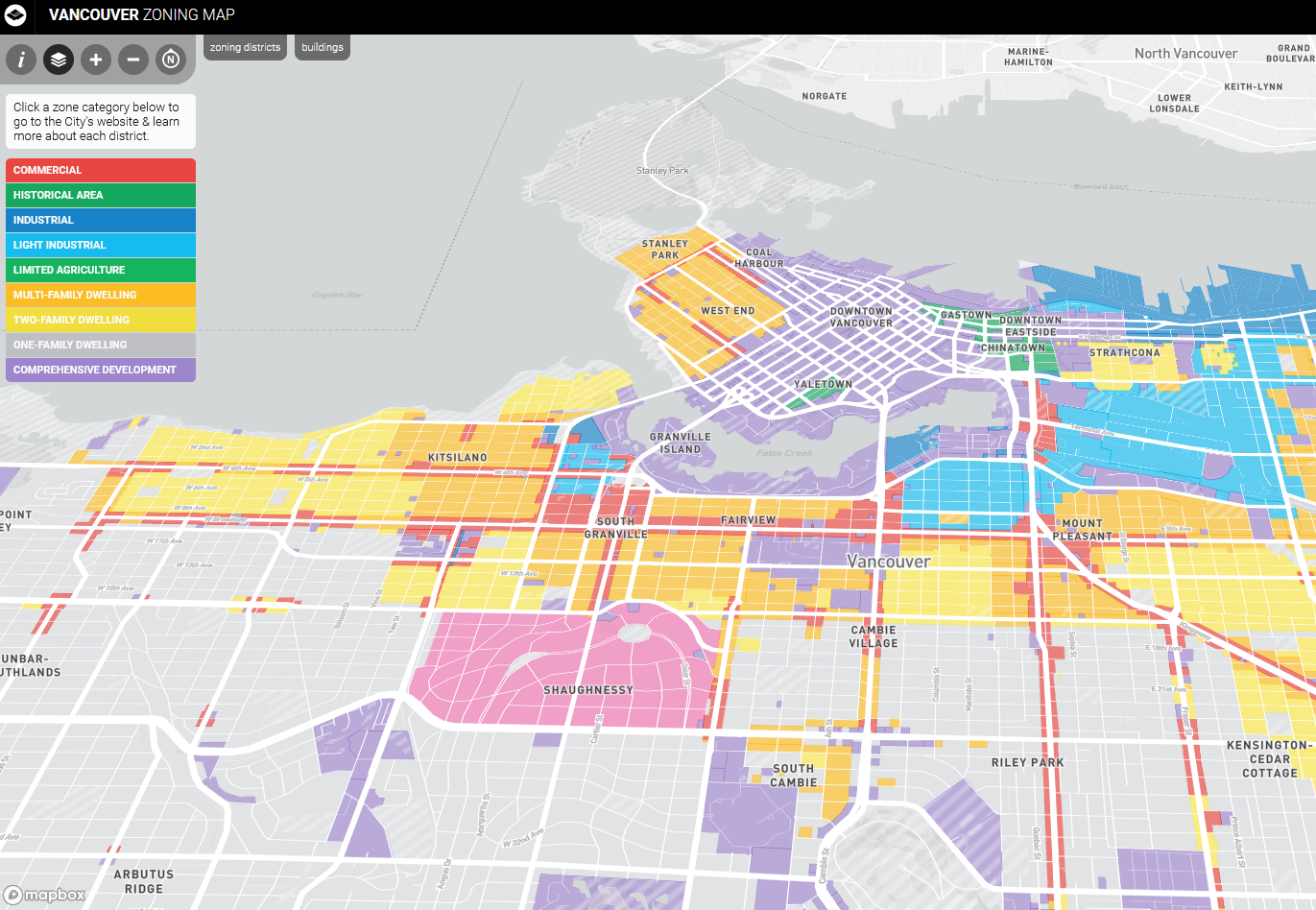
Nominal Scale
Names or categories with no ranking or direction. Categories are not more/less, better/worse, they just different. Some examples include:
- Flower Species
- Zoning Categories
- Land cover Classification

Nominal Operations
With nominal data we can:
- Check equivalency
- Count frequencies
- Nothing else

Ordinal Scale
Names or categories with a ranking. The differences are relative. Categories are more/less, better/worse, etc.
- Spice levels

Ordinal Scale
Names or categories with a ranking. The differences are relative. Categories are more/less, better/worse, etc.
- Spice levels
- Relative heights

Ordinal Scale
Names or categories with a ranking. The differences are relative. Categories are more/less, better/worse, etc.
- Spice levels
- Relative heights
- Compass Direction

Ordinal Operations
All the same operations as nominal data + more. With ordinal data we can:
- Check equivalency
- Count frequencies
- Check order/rank

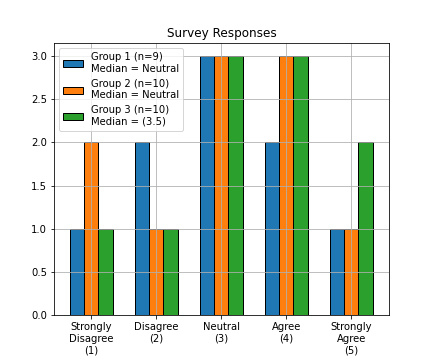
Ordinal Operations
Sometimes we can calculate the median.
- Odd sets the median is the middle.
- Even sets, average of the middle two.
- One solution, arbitrarily assign a numeric score.
Graded Membership
Exceptions that blur the lines. Where to draw the line between forest/alpine?
- Grade membership to assign categories
- Winner take all: alpine meadow
- 45% alpine meadow
- 40% forest
- 5% bare rock

Graded Membership
In practice, lots of qualitative data we work with, especially for natural phenomena, are actually graded membership.
- The downside: variability within the area is lost.

TopHat Question 2
Which of the following would be examples of Nominal Data? (select all that apply)
- Air temperature
- Ice cream flavors
- Tree height
- Colors
- Drink sizes
Quantitative Data
Quantitative data is Numeric. It describe the quantities associated with a phenomenon. Key properties include:
- Values separated by a meaningful unit.
- More arithmetic operations possible.
- Can be Discrete or Continuous numbers.
- Measured on either a Ratio or Interval scale.
Kinds of Numbers
Discrete
- Whole numbers
- Counts
- Not infinitely divisible
- Names in ArcGIS Pro:
- Integer, Long, etc.
Continuous
- Decimals
- Measurements
- Infinitely divisible
- Names in ArcGIS Pro:
- Float, Double, etc.
Kinds of Numbers
Discrete
- Countable
- Examples:
- Population
- Year
- “Age”
Continuous
- Non-countable
- Examples:
- Temperature
- Height
- Speed
Quantitative Data
Both Interval and Ratio data can consist of discrete or continuous numbers. These types of quantitative data are closely related, but have one important distinction.
- Interval scales have an arbitrary zero point
- Can be negative
- Cannot multiply/divide
- To compare magnitudes
- Ratio scales have a fixed, absolute zero point
- Can multiply/divide
- Cannot be negative
- Can increase infinitely from zero
Celsius (interval) vs. Kelvin (ratio)
°C = K-273.15.
- 0 °C: Freezing point of water
- Drops below 0 °C all the time
- 0 K: “Absolute Zero”
- Physically cannot get any colder
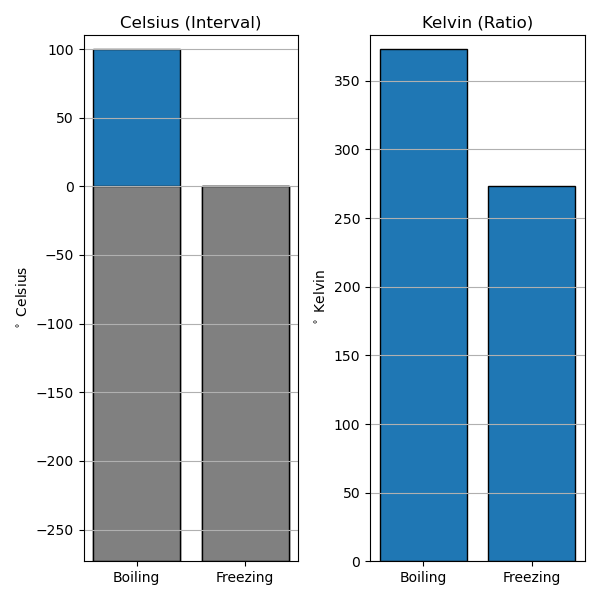
Celsius (interval) vs. Kelvin (ratio)
°C = K-273.15.
- 100 °C is not ∞% warmer than as 0 °C
- It’s actually ~ 36% warmer
- (373.15 K - 273.15 K) ⁄ 273.15 K ~ 0.36

Interval Scale
Interval data has an arbitrary zero point.
- Calendar years
- Discrete interval data
- Temperature (in celsius)
- Continuous interval data
- Other examples:
- ph scale (continuous)
- Times (discrete-ish)

Interval Scale
Interval data has an arbitrary zero point.
- Calendar years
- Discrete interval data
- Temperature (in celsius)
- Continuous interval data
- Other examples:
- ph scale (continuous)
- Times (discrete-ish)
Ratio Scale
Ratio data has a fixed, absolute zero point.
- Population
- Discrete ratio data
- Tree height
- Continuous ratio data
- Other examples:
- Precipitation (Continuous)
- Vote Totals (Discrete)
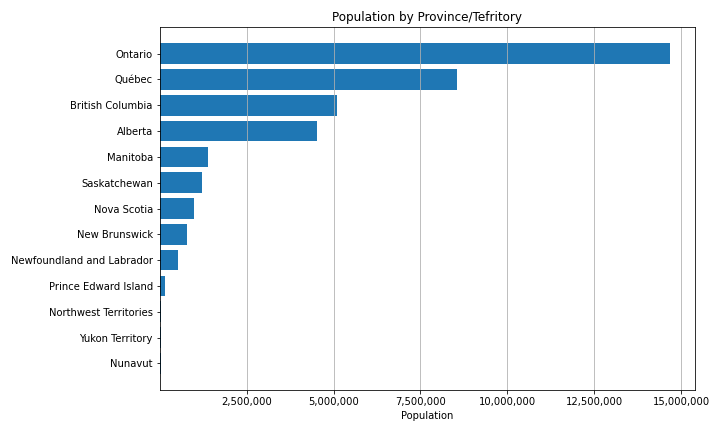
Ratio Scale
Ratio data has a fixed, absolute zero point.
- Population
- Discrete ratio data
- Tree height
- Continuous ratio data
- Other examples:
- Precipitation (Continuous)
- Vote Totals (Discrete)

TopHat Question 3
Match the value to the type measurement scale and type of number:
| Length a hiking trail | Interval (Discrete) |
| Temperature in Fahrenheit | Ratio (Discrete) |
| Global Orca Population | Ratio (Continuous) |
| Change in Global Orca Population from 2000 to 2022 | Interval (Continuous) |
Derived Ratio
Sometimes called normalizing or standardizing, we calculate derived ratios to account for the influence of a confounding variable over a variable of interest. e.x. Housing affordability (Ha):
- You need to account for income (I) to figure out how affordable rent (R) is: \(H\_a = \frac{R}{I}\)
- Ha: 31.5% of my income goes to rent
- Income and rent ($) are both discrete, housing affordability (%) is continuous.
Derived Ratio
In Lab, you are going to work with two derived ratios:
- Income and Food expenditures are correlated
- Need to account for income if you analyze other factors
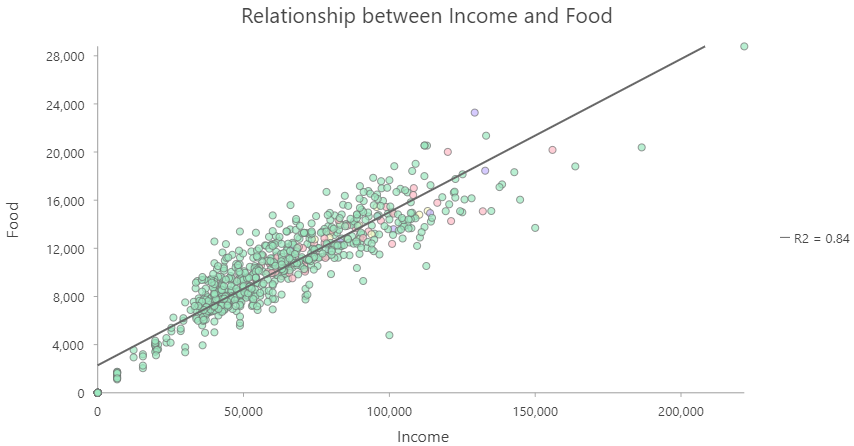
Derived Ratio
In Lab, you are going to work with two derived ratios:
- Population and Area are not highly correlated
- But area definitely influences population
- Need to account for area to analyze other factors
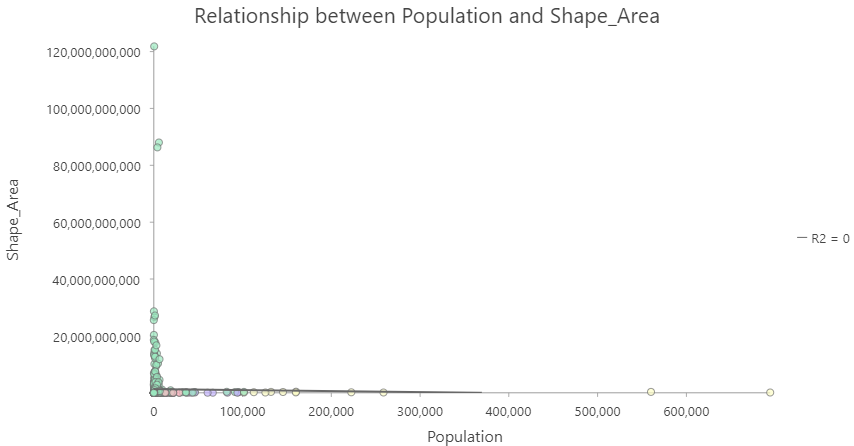
TopHat Question 4
Speed is another example of a derived ratio. If a line of thunderstorm takes 5 hours to travel from Brandon, MB to Winnipeg, MB (200 km), what is the storm’s speed in km/hr?
Summary: Types of Data

Summary: Operations
| Operation | Nominal | Ordinal | Interval | Ratio |
| Equality | x | x | x | x |
| Counts/Mode | x | x | x | x |
| Rank/Order | x | x | x | |
| Median | ~ | x | x | |
| Add/Subtract | x | x | ||
| Mean | x | x | ||
| Multiply/Divide | x |