Spatial Sampling
How do we collect geospatial information?
TopHat Question 1
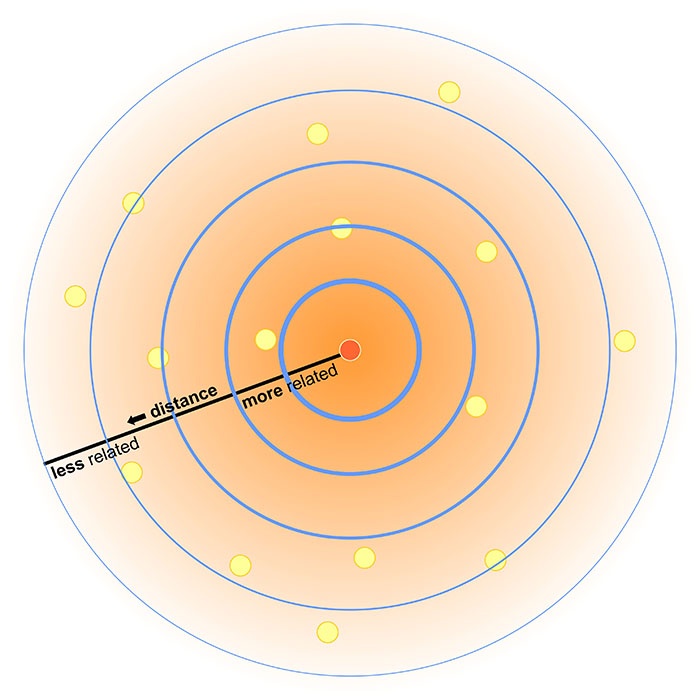
“Everything is related to everything else, but near things are more related than distant things.” This statement is known as:
- Tobler’s First Law of Geography
- Tobler’s Last Law of Geography
- Geography’s First Principal
- The Only Rule of GIS
The First Law of Geography
Everything is related to everything else, but near things are more related than distant things.
- Object/areas near each other are more likely to be similar Objects/areas near that are distant from each other are more likely to be different
- This aspect of nature keeps coming in GIS!
Sampling
The process of selecting points from within an area or population, called a sample frame.
- We collect information for a subset of objects/locations sample frame
- But we ignore most objects/locations
- Think back to Bonini’s Paradox
Sampling
The process of selecting points from within an area or population, called a sample frame.
- How we define the sample frame and choose samples can determine the quality of our data
- We want to maximize representativeness of the sample
- But also minimize effort and expense associated with sampling
Scientific Sampling
Requires each element in the sample frame have a known and pre-specified chance of selection.
- Biased Sampling: some elements have a greater or lower chance of being selected
- Unbiased: every element has an equal chance of being selected
Random Sampling
In theory, a random sample is best. Its the “gold standard”.
- Unbiased: each location has equal chance of selection
- Easy to do, randomly select 𝑥,𝑦 coordinates
- A key assumption of many statistical tests
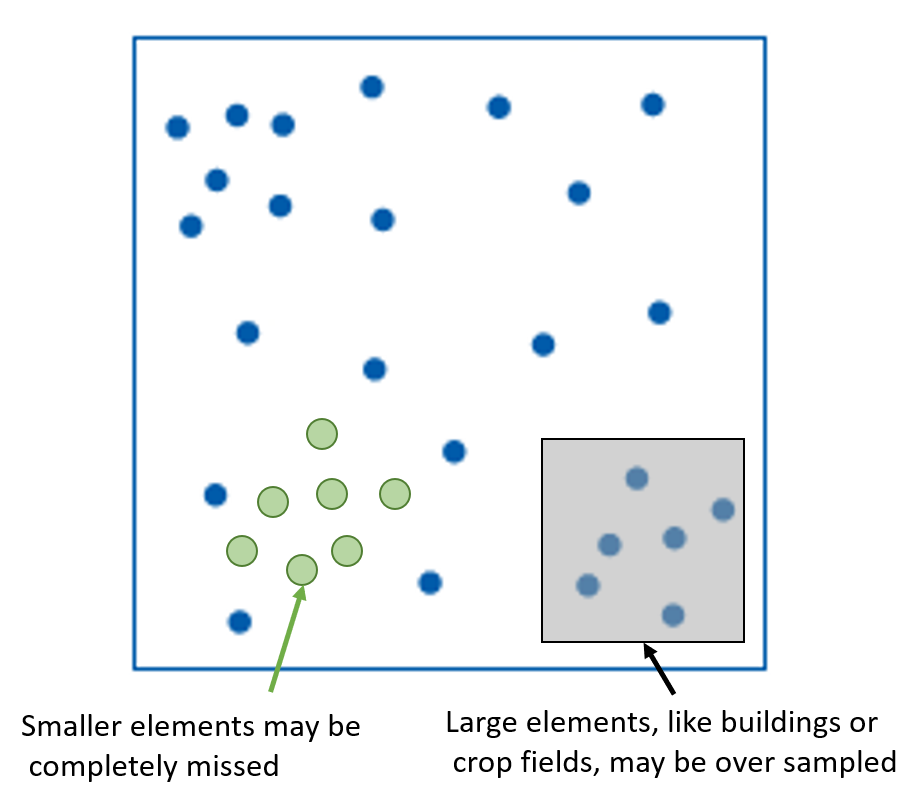
Random Sampling
Can be difficult to implement in practice.
- Chance that all samples miss important features
- May be barriers to access
- Remote or rugged terrain
- Private property
- Systematic under-responses

Random Sampling
We have some options to account for the drawbacks
- “Law of large numbers”: as we collect more information, our sample will become increasingly representative of actual population values
- Larger sample sizes or “Bootstrapping”
- Not always practical
- Requires more time and resources
TopHat Question 2
To collect a random sample, every object or location must:
- Have an equal chance of selection
- Be approximately the same size
- Not be close to other samples (i.e., equally dispersed)
- Not have a predefined chance of selection
Alternate Approaches to Sampling
Biased sampling
- Create a sample design that trades a sampling scheme for randomness
- Induce bias to the sample to:
- Save time or resources
- Account for relevant information about the sample frame
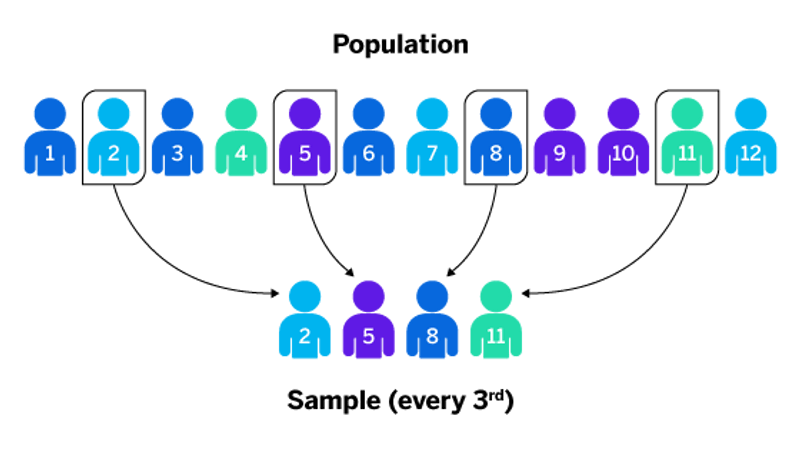
Systematic Sampling
A random starting point is chosen and a fixed sampling interval is used.
- Randomly select first of 3 students
- Select every 3rd after
Systematic Sampling
A random starting point is chosen and a fixed sampling interval is used.
- Choose a random starting point
- Then draw equally spaced grid
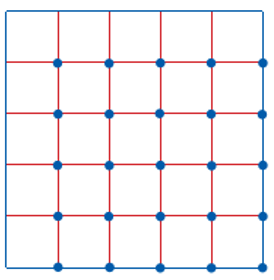
Systematic Sampling
A random starting point is chosen and a fixed sampling interval is used.
- Premise behind satellite data collection
- Often good for continuous fields
- eg., land cover
- Often good for continuous fields
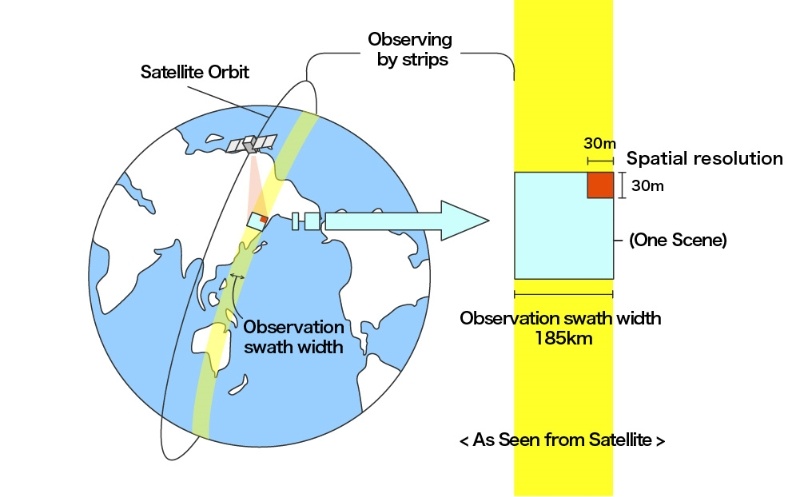
Systematic Sampling
A random starting point is chosen and a fixed sampling interval is used.
- Not ideal for discrete objects that exhibit periodicity
- City blocks, Roads, etc.
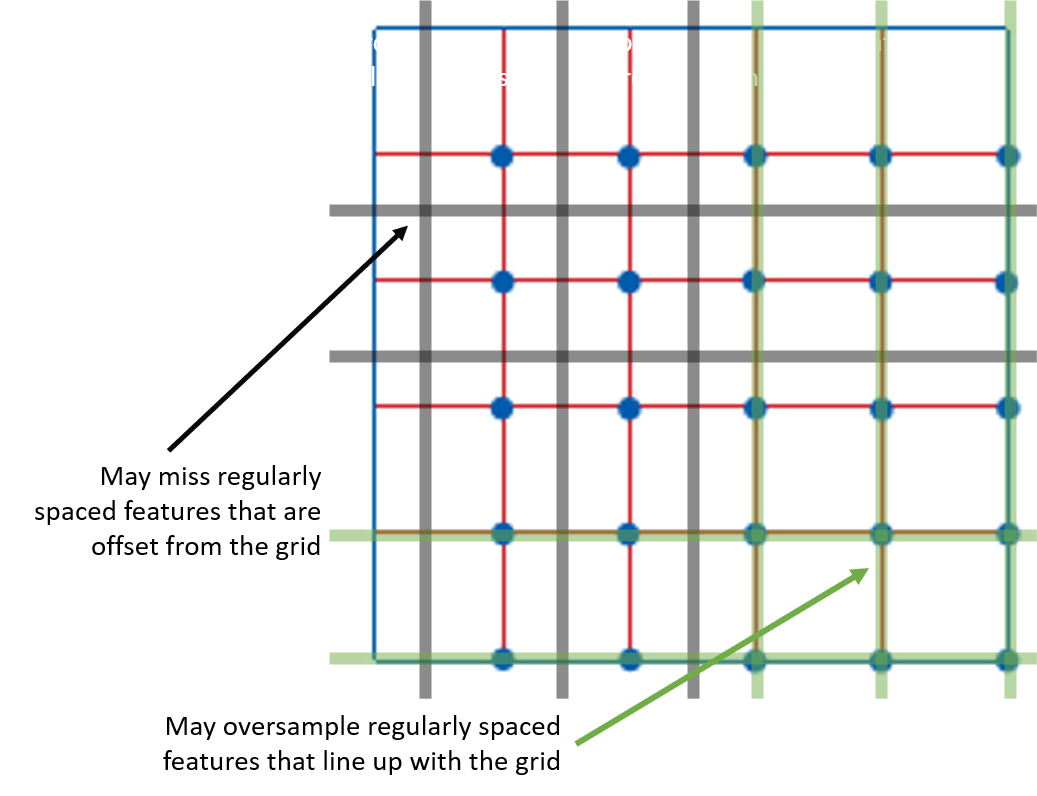
Stratified Sampling
Address the issues with systematic sampling by sampling at random locations, while applying a “systematic bias”
Create a systematic sampling grid, then take random samples within cells
Can avoid over/under sampling regularly repeating features
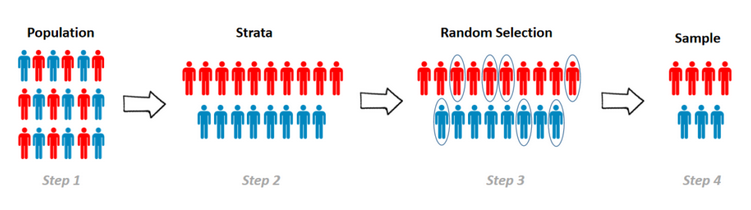
Stratified Sampling
Divide a population by certain attributes, then take random samples from sub-populations
- Account for important factors
- Gender, race, age, political party, etc.
Cluster Sampling
Intense sampling of features in clusters around a number of selected locations
- Locations can be selected for specific features, e.g.,:
- Shopping centers
- Known history of invasive species
- Or, locations can be selected at random across the grid
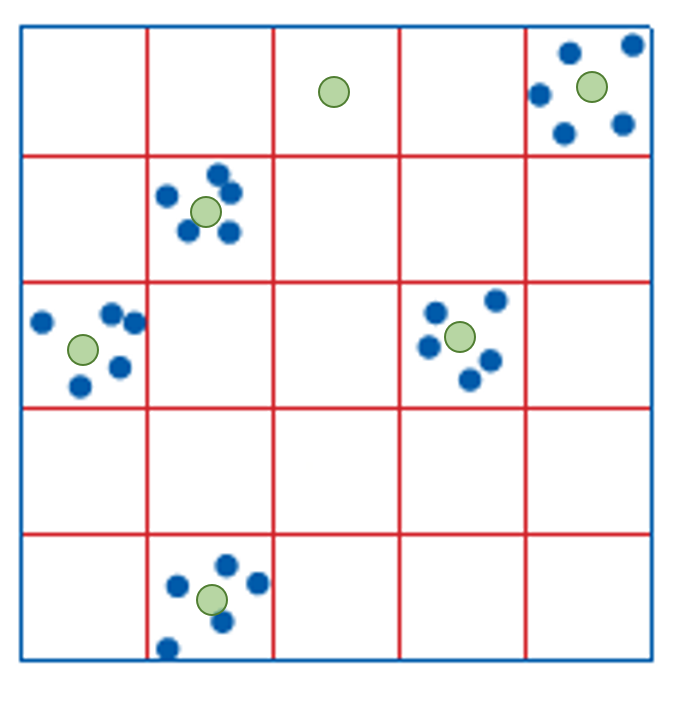
Cluster Sampling
Intense sampling of features in clusters around a number of selected locations
- More efficient use of time and resources
- May not be representative

Transect Sampling
Commonly used along line features like roads & rivers.
- Focused effort on features of interest
- Requires understanding of spatial structure for maximum effectiveness


TopHat Question 3
Which of these sampling methods are unbiased?
- Cluster
- Stratified
- Transect
- Random
How Many Samples?
The number of samples required is a function of how similar units of that population are.
- Spatial structure can vary wildly across a landscape
- Knowledge of your study area will help to establish how to best sample
- Maximize returns minimize effort

Spatial Autocorrelation
When the values of objects are related to the values of nearby objects.
- If you know the value of one object, you can make a reasonable guess at the value of nearby objects

Spatial Autocorrelation
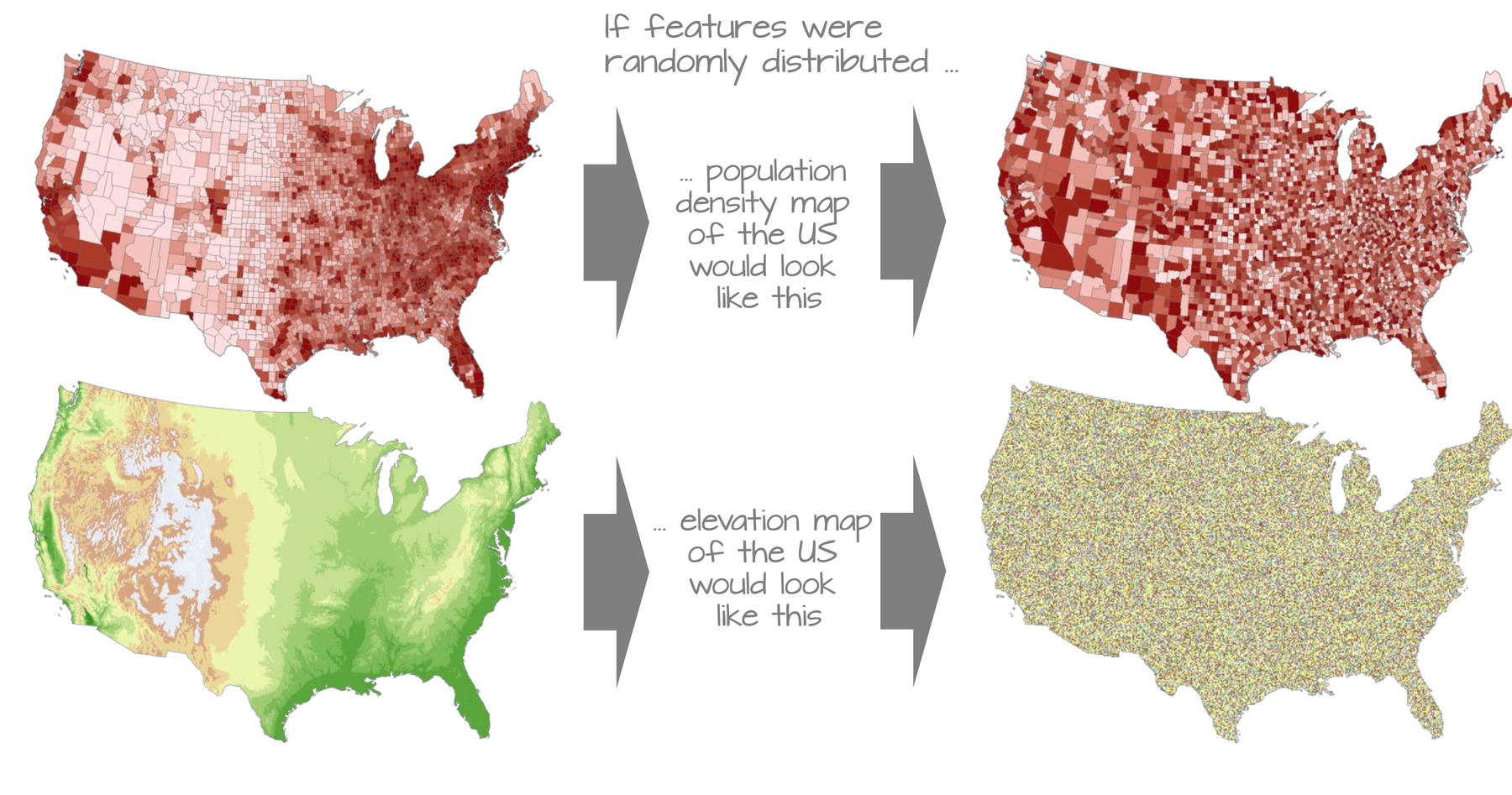
Spatial Autocorrelation
Correlation does not imply causation!
- There could be relationship between features
- Or a relationship to a third object that determines the values of both
- Or a completely random coincidence
Statistical Assumptions
Spatial autocorrelation is a problem when it comes to spatial statistics.
- Most tests assume that there is no relationship between objects by default!
- By violating this assumption, we “break” many common statistics!
- Spatial statistics explores ways of analyzing statistical relationships across space
TopHat Question 4
Which number completes the sequence: 2, 4, 6, __, 10?
- 3
- 8
- 11
- 100
Statistical Interpolation
The process of “filling in the blanks” that you just performed is called interpolation
If you know the value of one object, you can make a reasonable guess at the value of nearby objects
Over a 2D or 3D surface we call this spatial interpolation
Intelligent guesswork in which we attempt to make reasonable estimates of the values of a continuous field at places where we do not have measurements
Spatial Interpolation
Spatial interpolation only makes sense for a continuous field with numeric values.
- Rainfall, temperature, pressure, elevation
- Estimate between measured locations
- Can be problematic with qualitative data
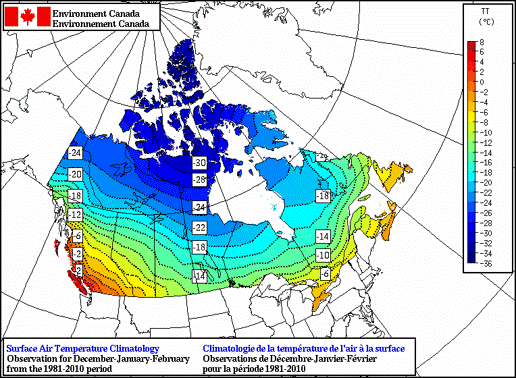
Spatial Interpolation
Continuous fields tend to exhibit strong positive spatial autocorrelation
- Reasonable to assume missing values are similar to those around them
- Methods incorporate distance to known samples.
- Sound familiar? This is Tobler’s First Law!
- Closer samples given more weight than distant ones
- A threshold is usually set, to determine the maximum distance to take samples from
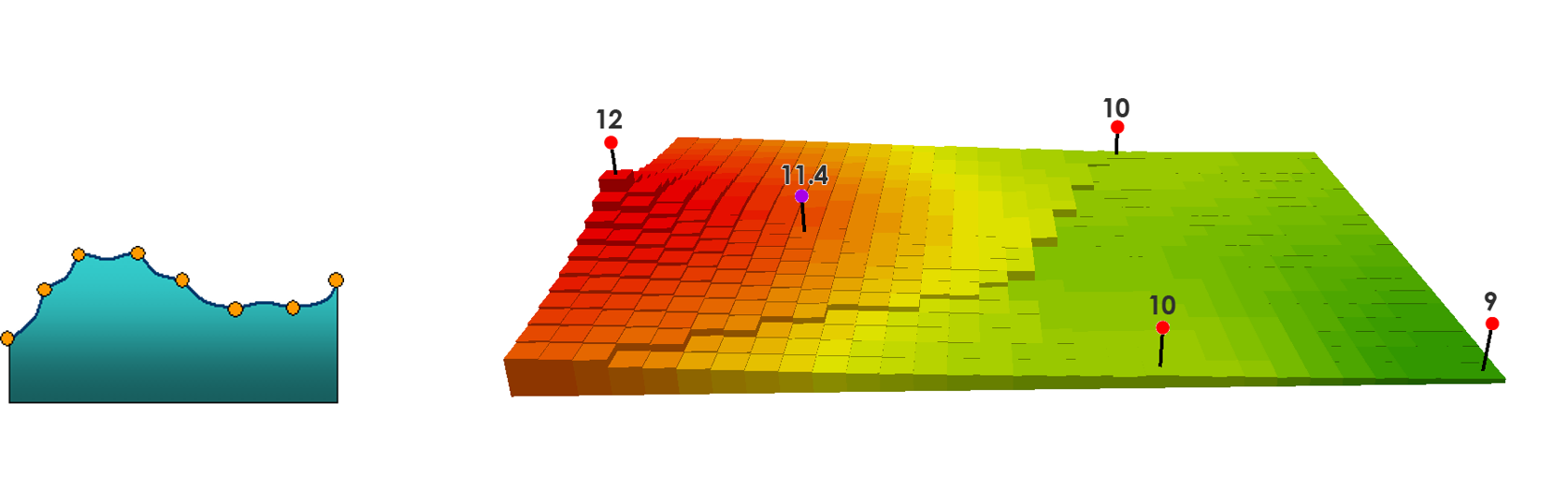
Inverse Distance Weighting
Calculates cell values based on nearby observations.
- Weight cells by distance from observation points
- Mathematical expression of Tobler’s Law
Inverse Distance Weighting
Best applied to discrete samples of continuous quantitative variables.
- Elevation
- Temperature
- Precipitation

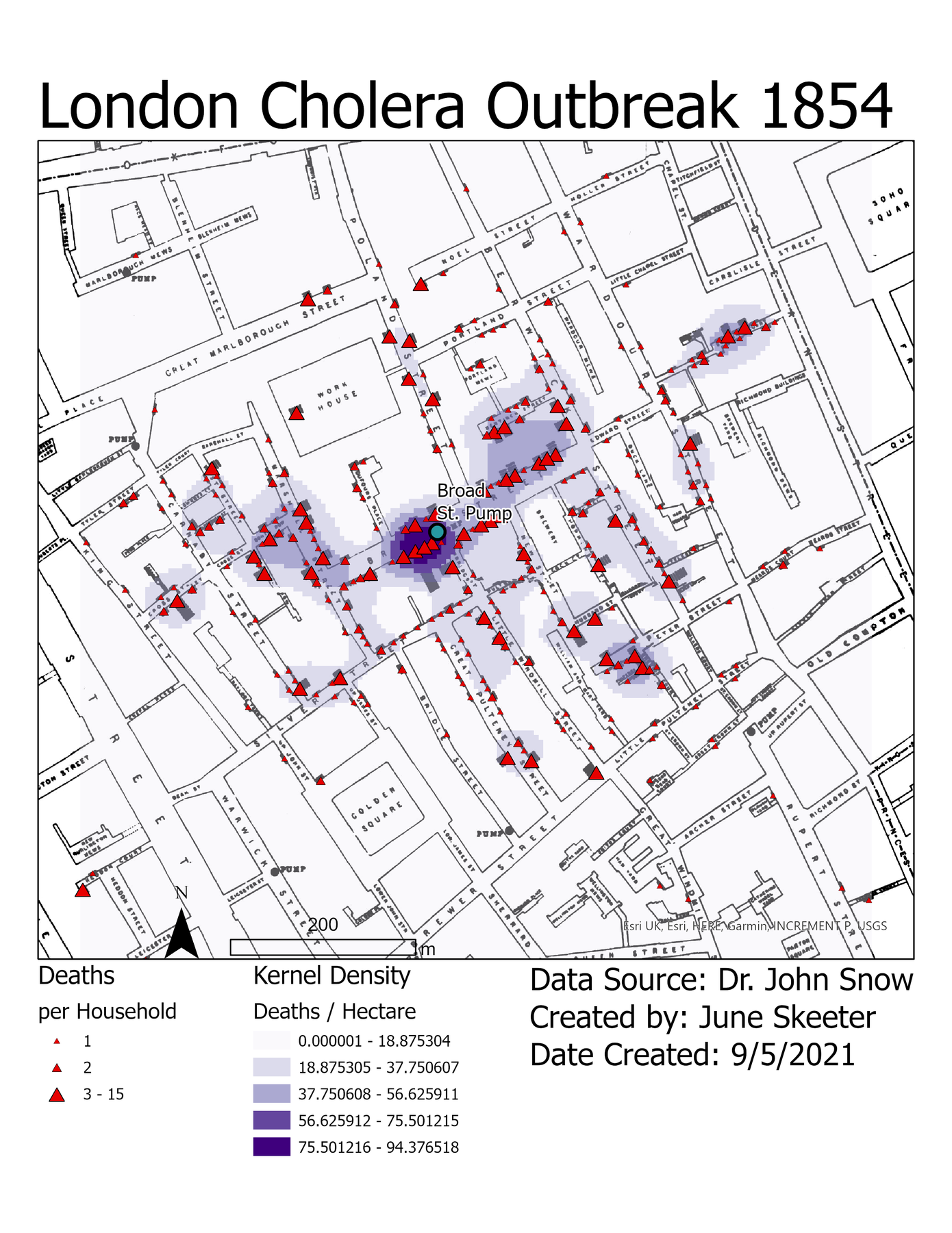
Kernel Density
Calculates the “density” of discrete objects and converts to a raster surface
- Probability of occurrence across space
- Weight by “value” of points
- Often applied to counts of qualitative data
- Disease outbreaks & crime data