Spatial is Special
Spatial data has special properties that we must take into consideration
First Law of Geography
“Everything is related to everything else,
but near things are more related than distant things.”
-Waldo Tobler
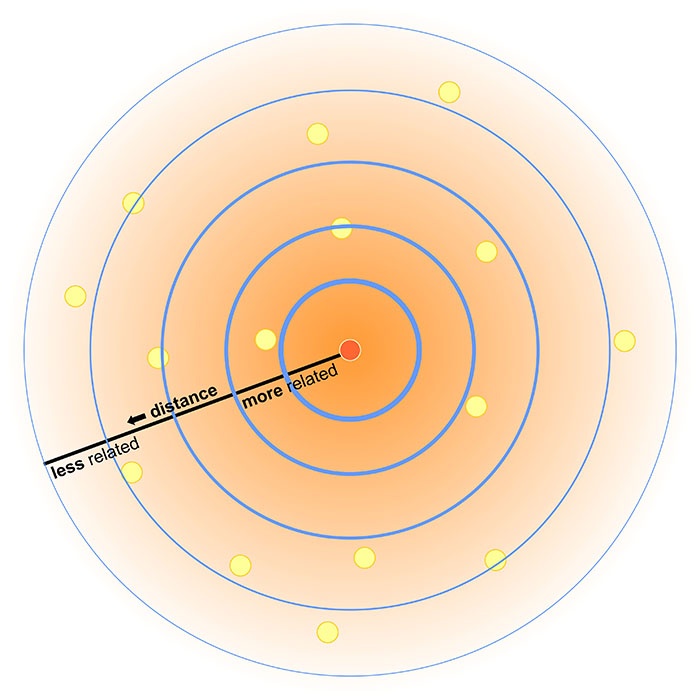
First Law of Geography
This might seem obvious:
- Students in the same class interact more.
- Orca pods in different areas develop different dialects.
- Hemlocks in BC are more related to each other than to hemlocks in NB.

First Law of Geography
Not a grantee of similarity.
- Vancouver’s average snowfall is < 30 cm/yr
- Grouse Mountain frequently exceeds 9 m/yr

First Law of Geography
What do you have in common with your neighbor?
- Are you in the same city?
- Do you have the same major?
- Are you from the same hometown?

TopHat Question 1
Everything is related to everything else, but …
- near things are less related than distant things
- near things are more related than distant things
- near things are aren’t related than distant things
Spatial Homogeneity
Even distribution of discrete objects trough space, or values (qualitative or quantitative) across a continuous field.

Spatial Heterogeneity
Uneven distribution of discrete objects trough space, or variation of values (qualitative or quantitative) across a continuous field.
- Opposite of Spatial Homogeneity
Spatial Heterogeneity
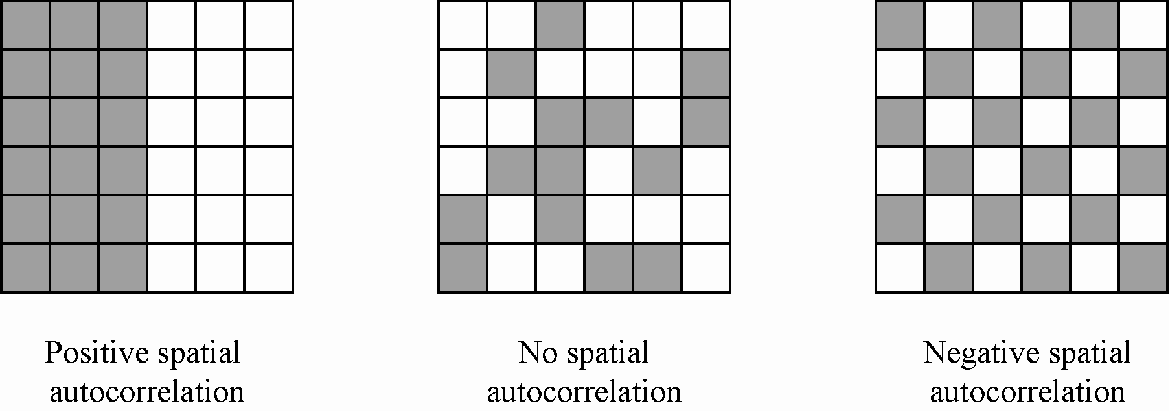
Spatial Autocorrelation
A measure of similarity Homogeneity/heterogeneity.
- Positive: Clustered/grouped in space
- Negative: Dispersed across space
- Many natural systems exhibit positive spatial autocorrelation
Spatial Autocorrelation
TopHat Question 2
These phenomena tend to exhibit a high degree of spatial autocorrelation (select all that apply)
- Air Temperature
- Elevation
- Precipitation
- COVID Cases
- Randomly Selected Samples
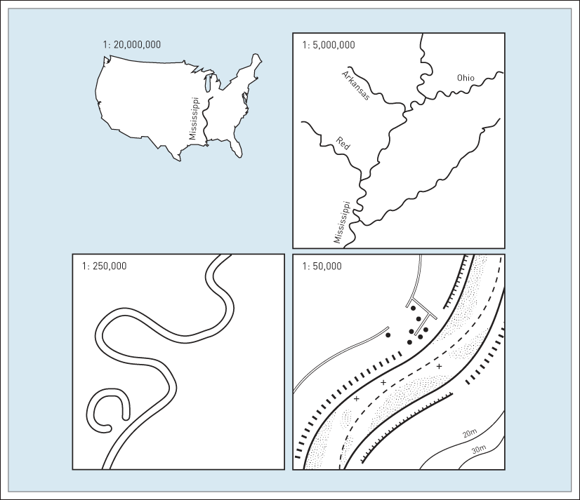
Revisiting Scale
Map scale: ratio of map units to real world units.
- Small Scale: Large area, more generalization, less detail.
- Large Scale: Small area, more detail, less generalization.
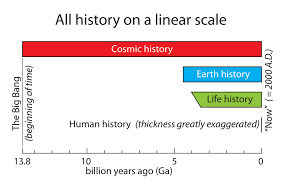
Time Scale
Time is “one dimensional”, but many of the same concepts related to scale apply.
- Just as features are exhibit spatial autocorrelation, they typically exhibit temporal autocorrelation
Analysis Scale
Different phenomena operate on different temporal and spatial scales.
- No need to model tornadoes in a global climate model.
- Impractical to map turbulence globally.
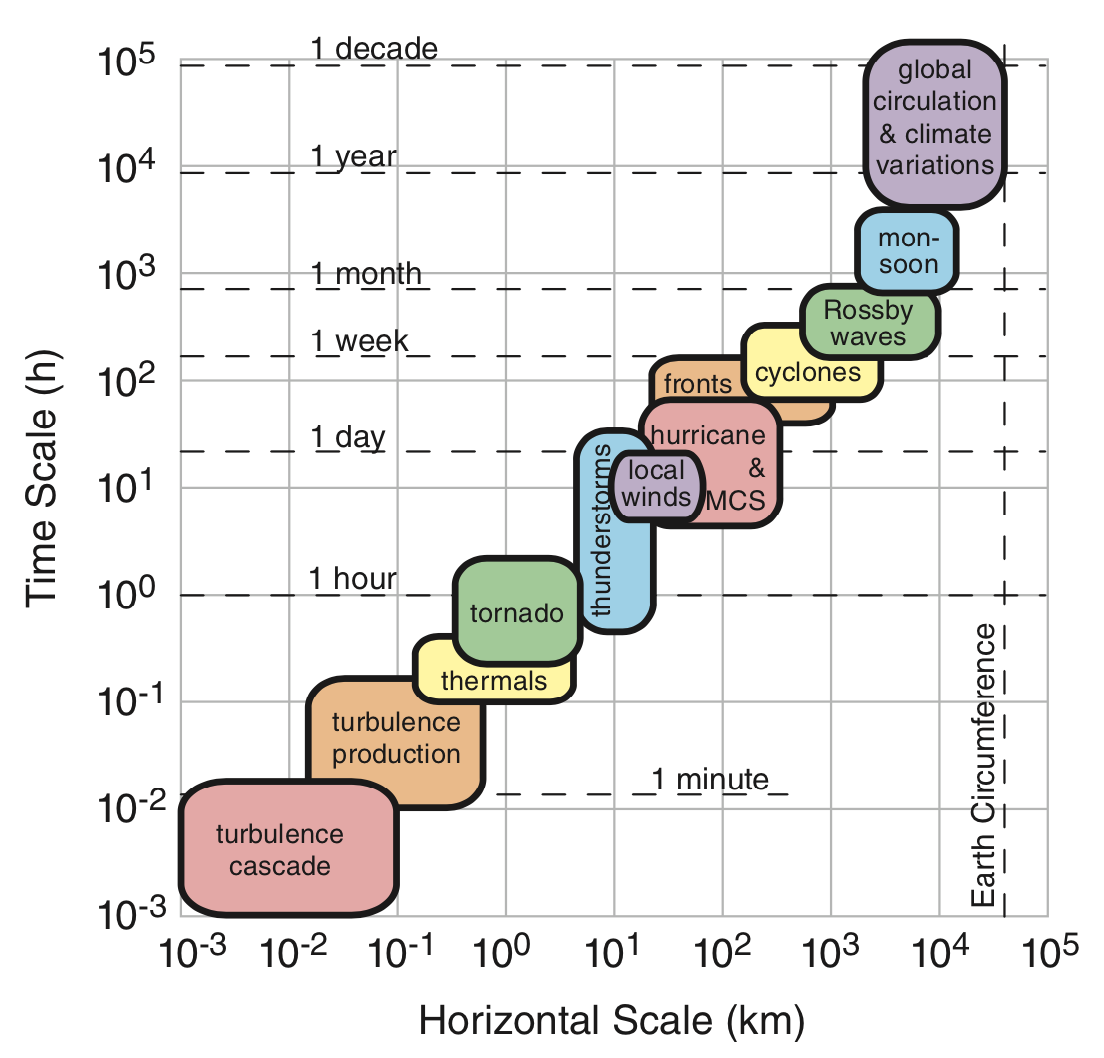
Analysis Scale
Different phenomena operate on different temporal and spatial scales.
- Identify the scale relevant to your analysis.
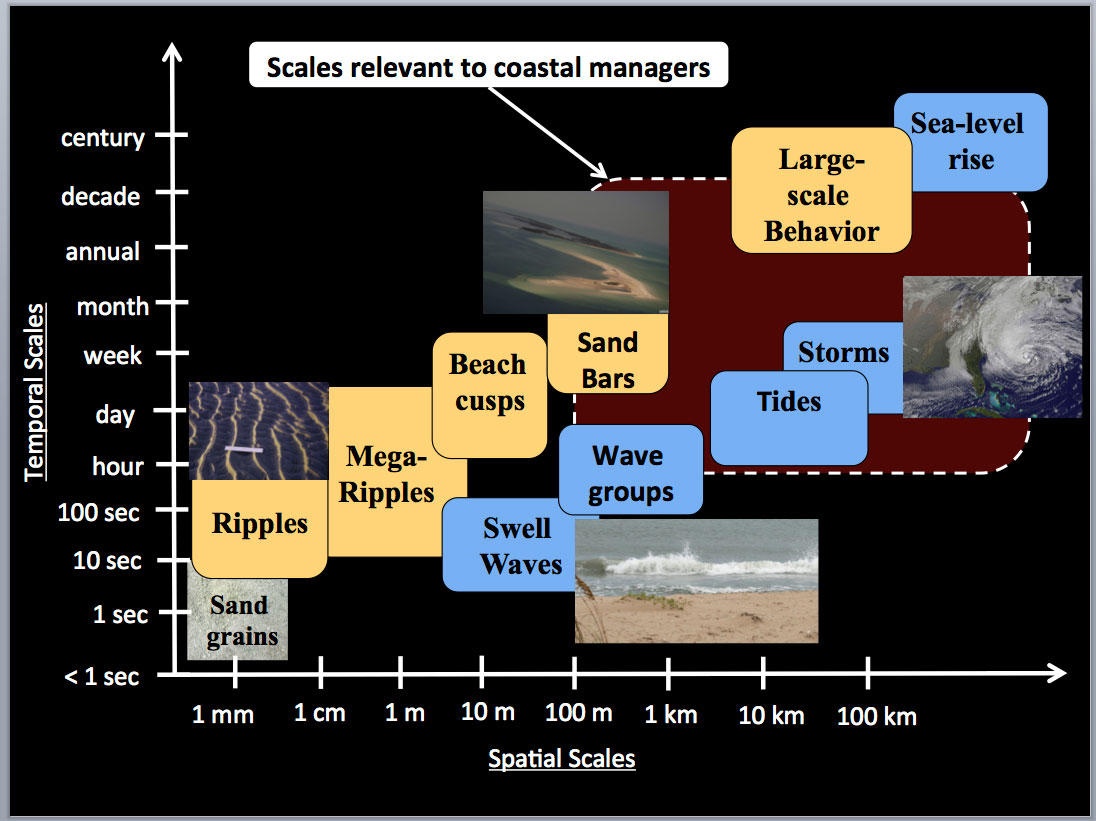
TopHat Question 3
Tobler’s First Law of Geography applies to time just as it applies to space.
- True
- False
Bonini’s paradox
As a model of a complex system becomes more complete, it becomes less understandable.
- It will eventually be just as difficult to understand as the real-world processes it represents
- A 1:1 scale map is as big as the feature you’re mapping
- A life size model house … is the size of a house
- At a certain point, we have to ignore the heterogeneity.
Map the Forest not the Trees
We don’t need the location of every tree to map a forest.
- Use average presence of trees over a larger area
- Group by dominant species or category

Similarity Across Space
Often, the system we want to map will exhibit high degrees of both spatial heterogeneity and autocorrelation.
- What is heterogeneous at one scale may be homogeneous at another.
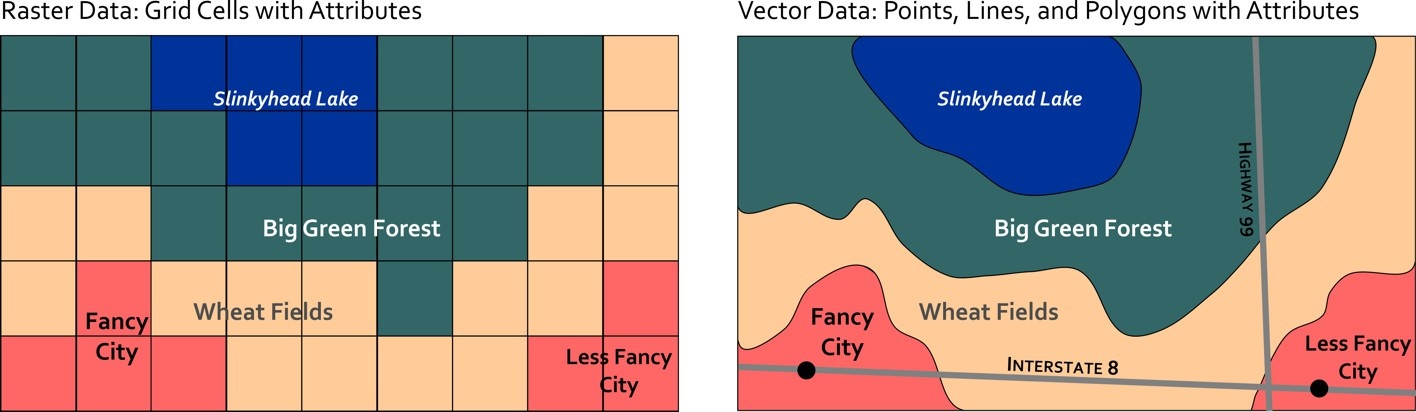
Spatial Data Models
We can exploit spatial autocorrelation to simplify data representation.
Spatial Resolution
Relates to the level of spatial detail in a dataset.
- What is the smallest feature that is included in a dataset?

Temporal Resolution
Relates to the level of temporal detail in a dataset.
- Over what time period is the data valid?
- Are there multiple observations?
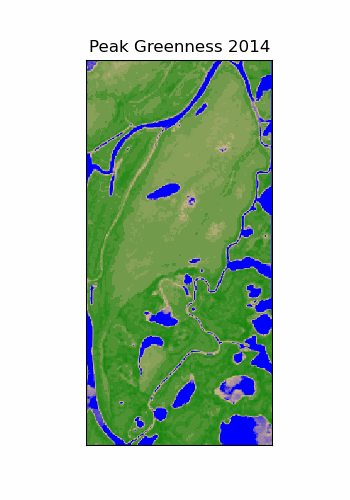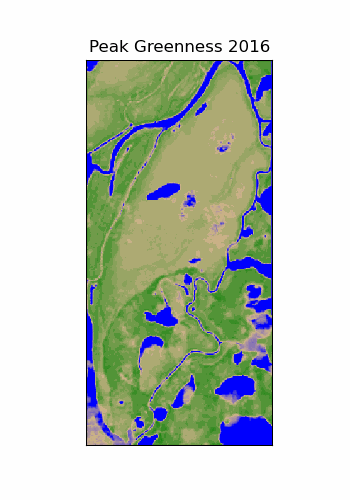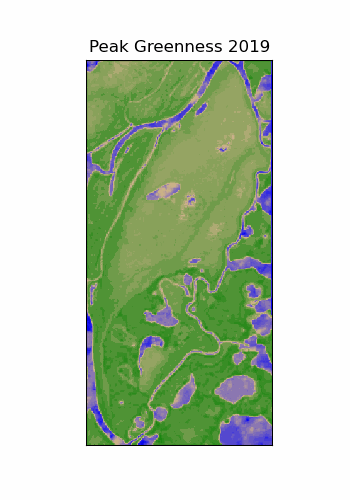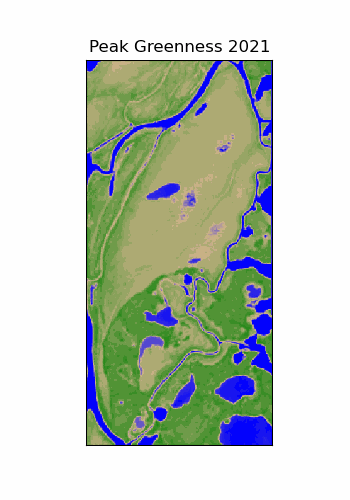
Resolution vs. Scale
The scale of our analysis dictates our desired resolution. But data resolution can limit the scale of our analysis.
Scale Dependence
Scale Dependence
Acknowledge heterogeneity where appropriate.
- Large scale maps might need more attention to detail.
- Higher resolution data.

Scale Dependence
Count on spatial autocorrelation
and call a unit homogeneous where appropriate.
- Smaller scale maps can be more generalized.
- Lower resolution data.
Scale Dependence
At even smaller scales, more and more generalization is required.
- Some features become indistinguishable
- Even lower resolution data is sufficient
Spatial Data Models
Raster and vector models are distinct approaches for addressing the same task.

TopHat Question 4
Spatial data models exploit spatial autocorrelation to simplify our representation of spatial features.
- True
- False