Map Projections
Types of projections and what we use them for.
Projected Coordinate Systems
A map projection is a transformation applied to a geographic coordinate system (GCS).
- Allows us to "convert" from 3D coordinates (Lat/Lon) to 2D coordinates (meters)
- Why does this work?
- While the GCS is a 3D coordinate system, it only references locations on the surface of the oblate spheroid
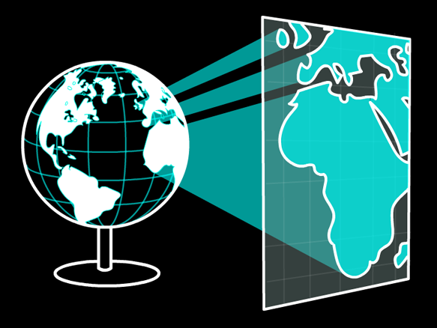
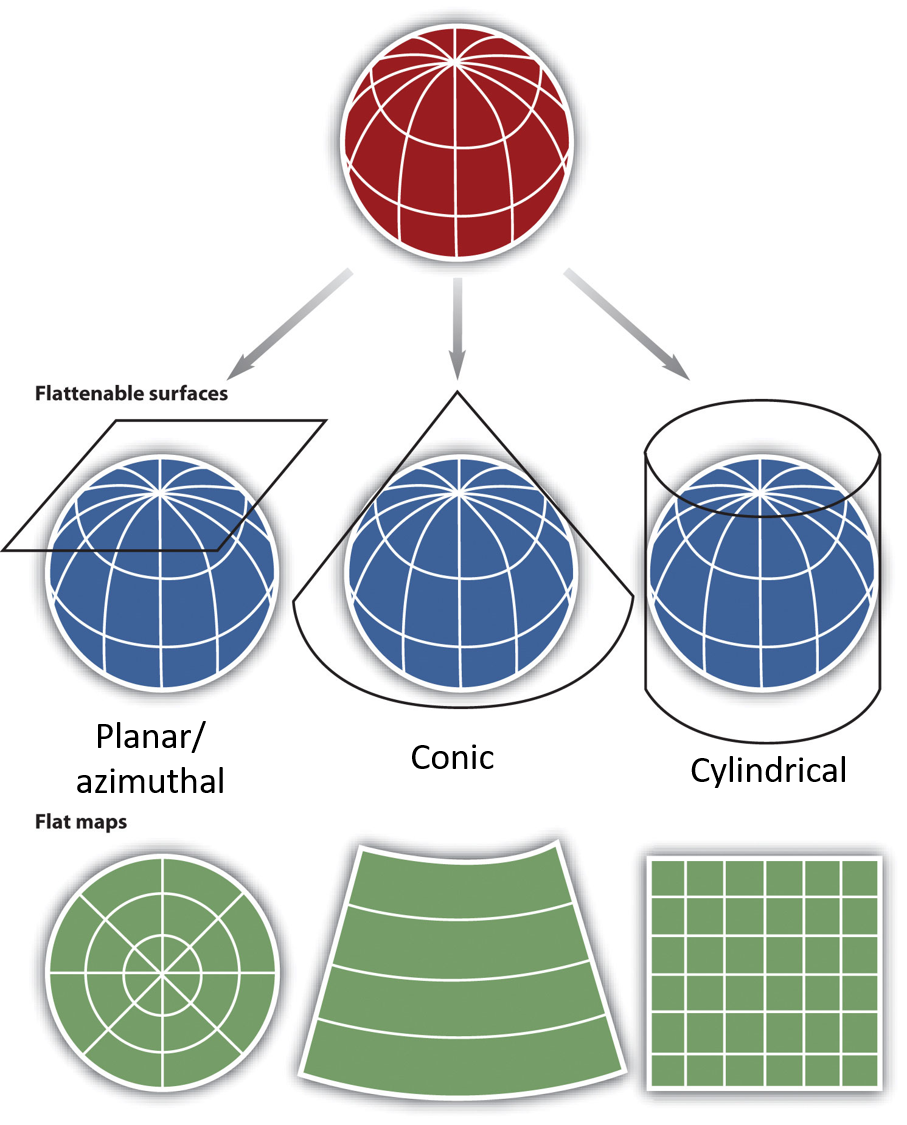
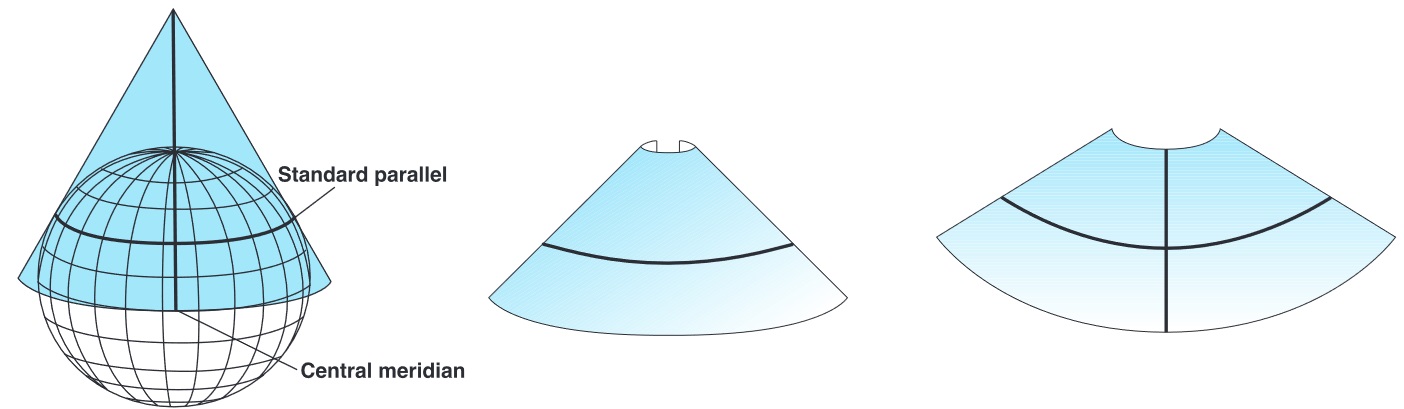
Projection Methods
There are three main ways to project the 3D oblate spheroid onto a 2D plane.
- Planar: A plane is referenced to "Earth's" surface
- Conic: A cone is referenced to "Earth's" surface
- The cone must be cut to flatten it
- Cylindrical: A cylinder is referenced to "Earth's" surface
- The cylinder must be cut to flatten it
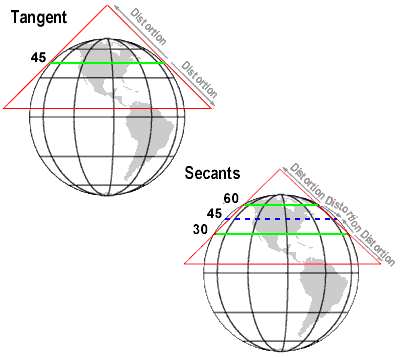
Projection Methods
How/where to reference the surface influences how the map is distorted.
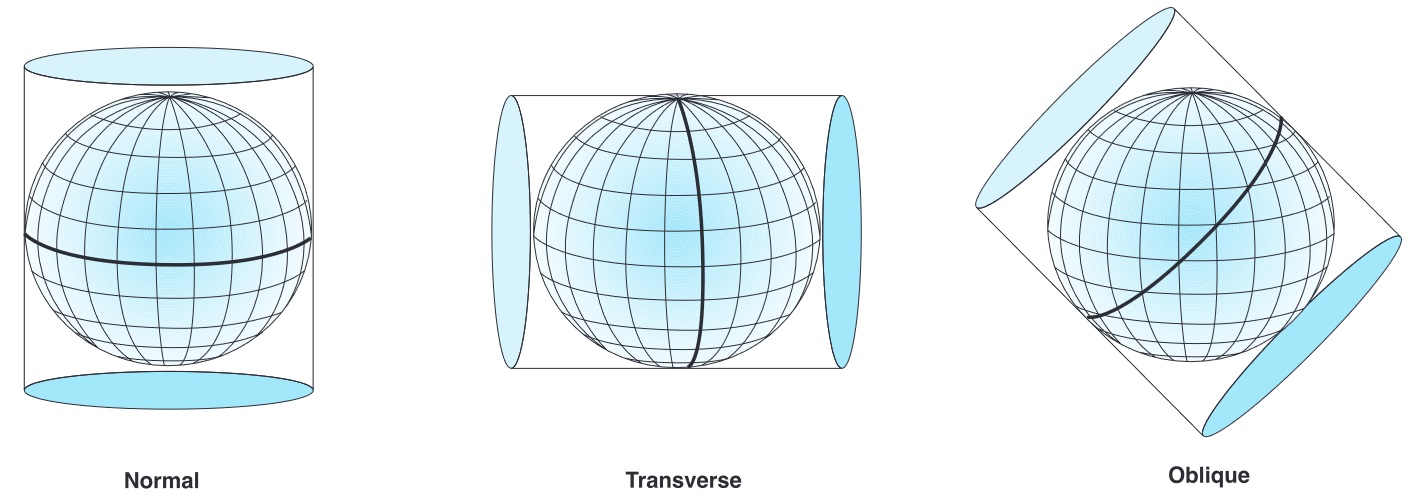
- Tangent: when projections touch the "earth's" surface at a one point or line
- Point for planar projections, line for conic and cylindrical projections
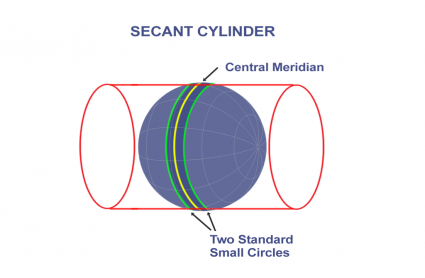
- Secant: when projections touch the "earth's" surface along two lines
- Helps minimize reduce distortion
- These are the only locations on map without distortions
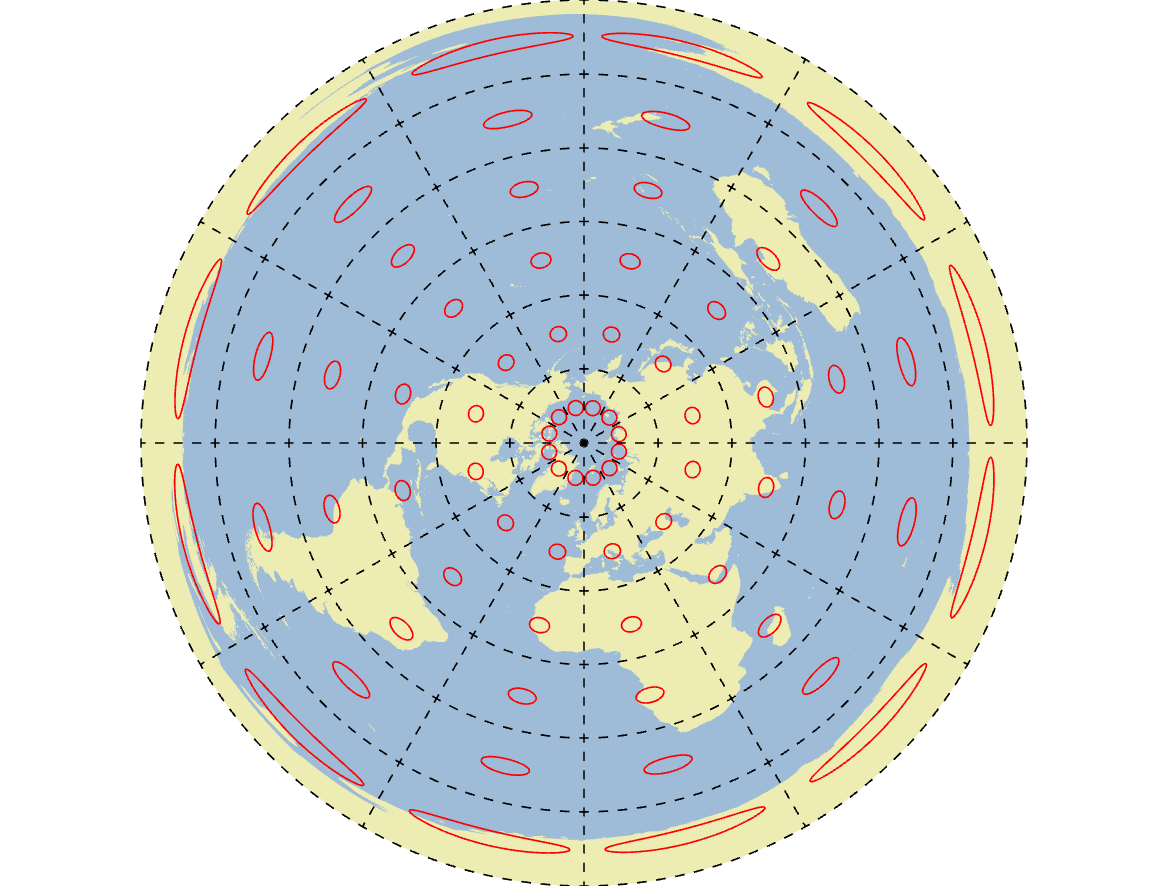
Planar Projections
Sometimes also called azimuthal or zenith projections, planar projections are the simplest approach.
- Limited applicability/scope and are typically only used for polar regions.
Planar Projections
The Polar Azimuthal projection, tangent to the north pole.
Conic Projections
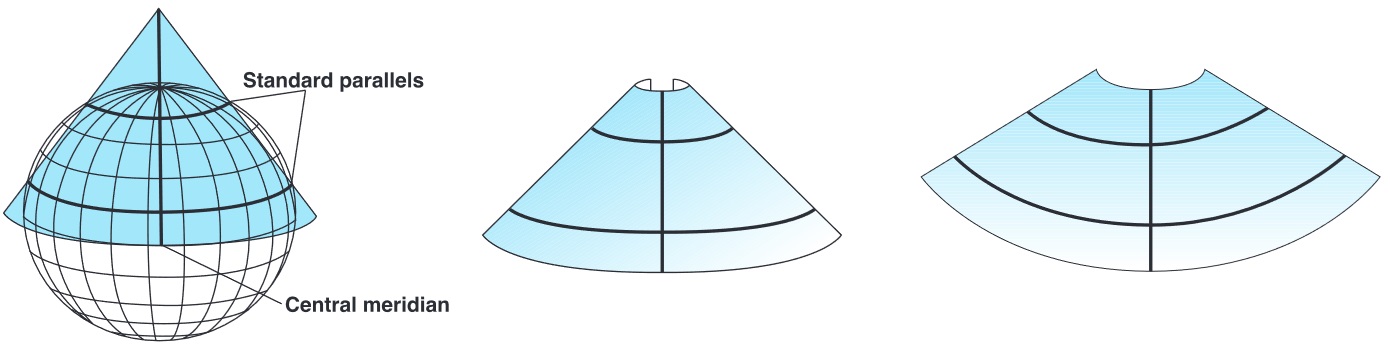
Conic projections are a great option for the mid-latitudes. They have one central meridian and one/two standard parallel(s).
- Can only cover one hemisphere at a time
Conic Projections
The BC Environment Albers projection, secant to 50° N and 58° N, central meridian 126° W.
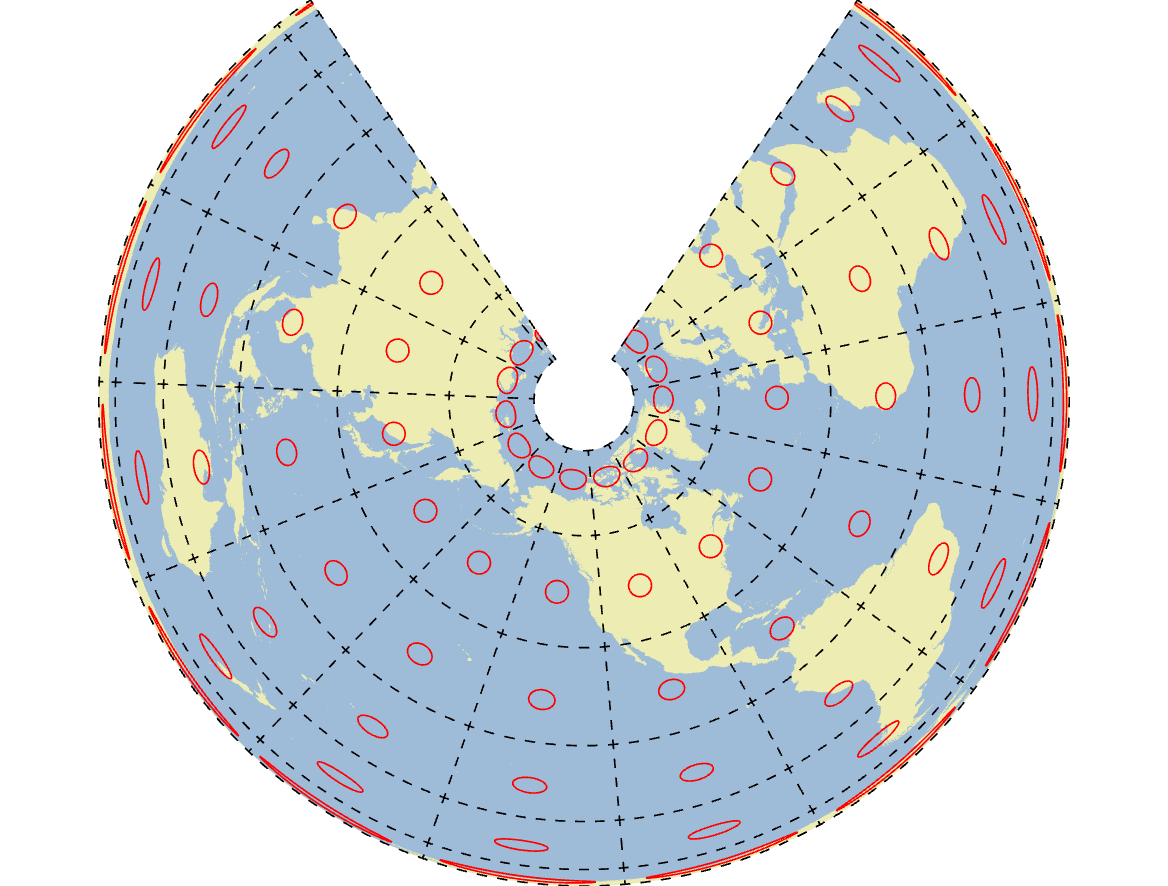
Conic Projections
Canada's "official" map projection: Canada Lambert Conformal Conic
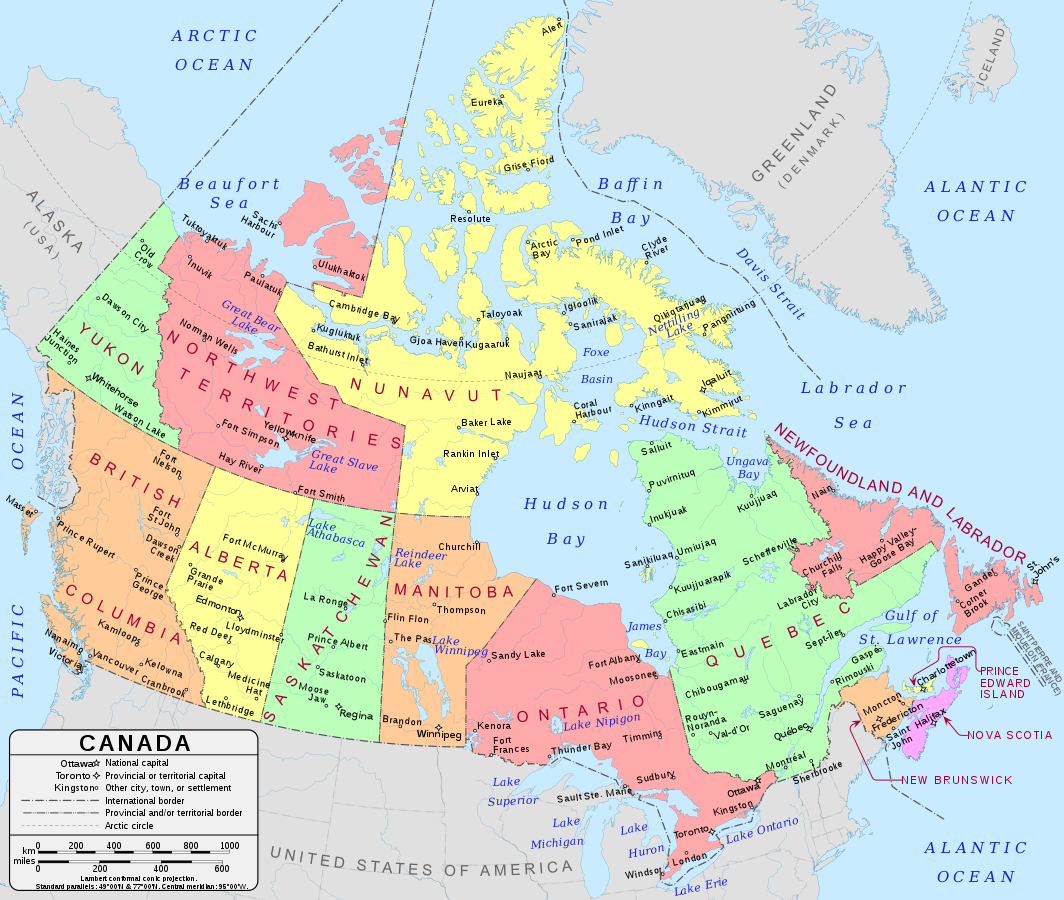
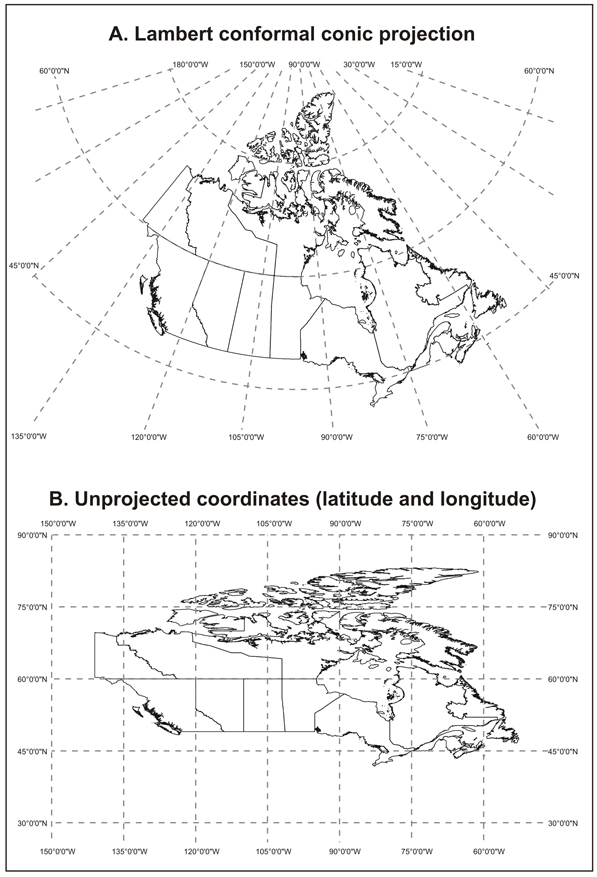
TopHat Question 1
A secant conic projection has one standard parallel while a tangent conic projection has two.
- True
- False
Cylindrical Projections
The only method that works (well) for displaying the full Earth.
Cylindrical Projections
The Mercator projection, tangent to 0° N and, central meridian 0° W.
Cylindrical Projections
Transverse cylinders projections are also frequently used.
- Minimize distortion near secant lines
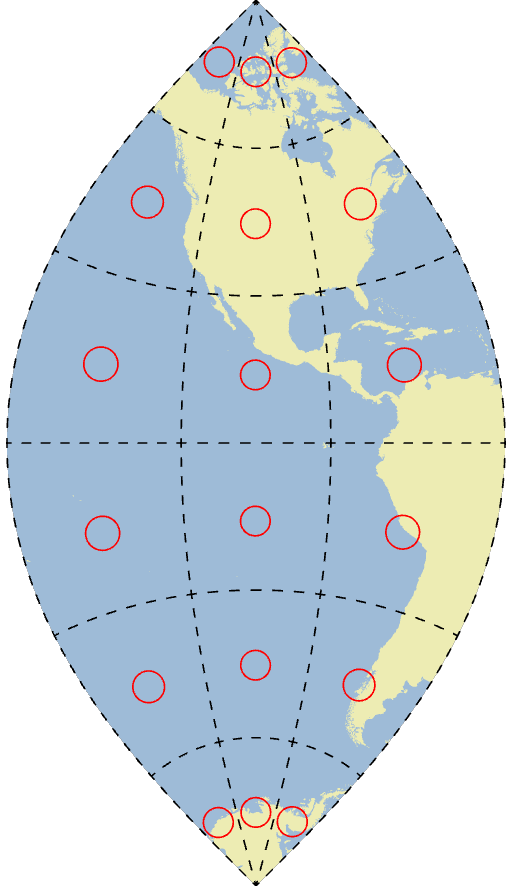
Pseudocylindrical Projections
Some special projections apply more complex transformations.
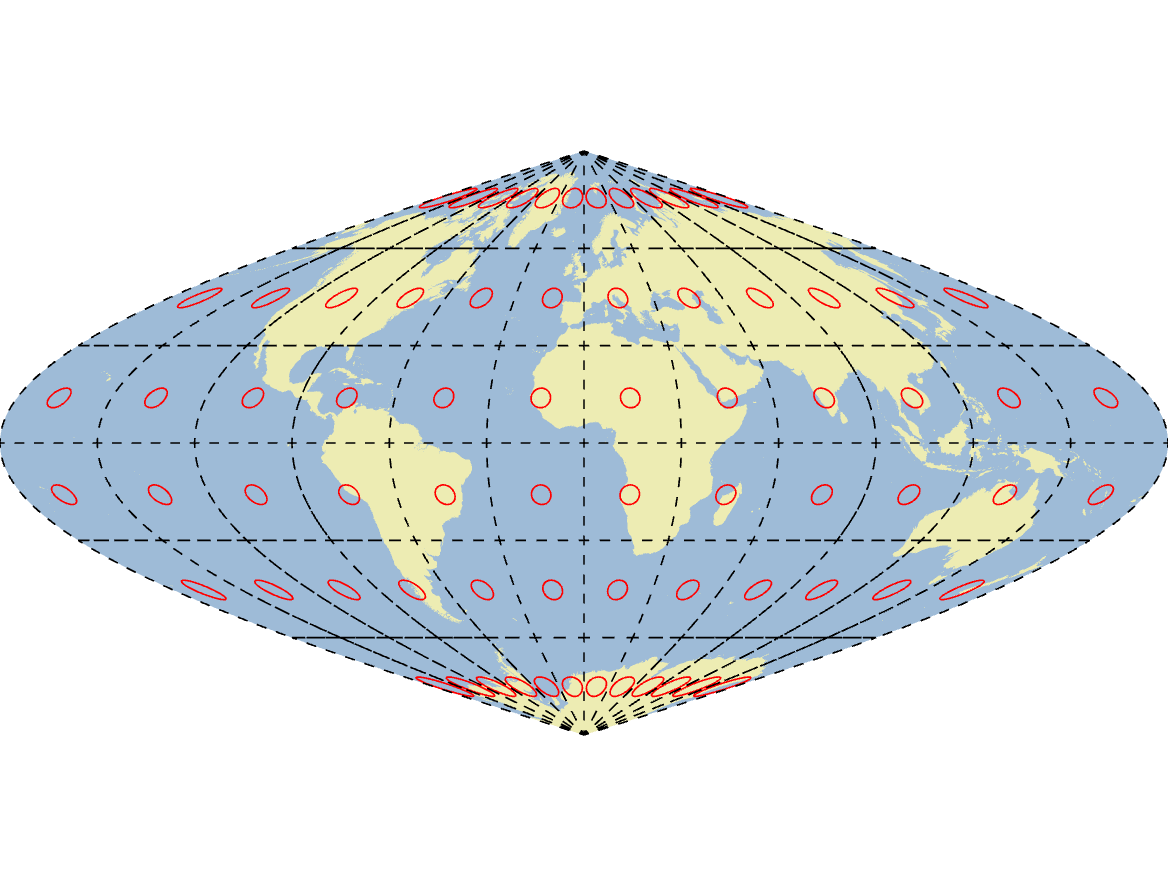
These tend to be used less frequently.
- Won't be used in this class

TopHat Question 2
Which of the these methods for projecting spatial data are best for global scale maps?
- Cylindrical
- Conic
- Planar
- Azimuthal
Types of Deformations
All map projections must induce distortions in order to display the 3D earth in 2D, they can cause different distortions in different ways:
- Tearing: All projections have tearing (edges)
- Shearing: Shapes and angles are contorted
- Compression: Changes to area
- Bit of a misnomer, often results in expansion
Tearing
All projections require tearing, some projections have more than others.
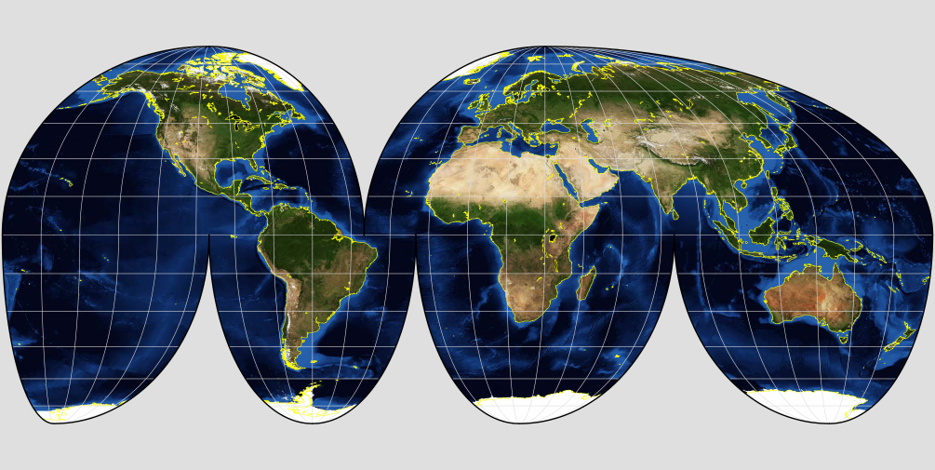
Shearing
Shapes and angles are contorted by some, but not all projections.

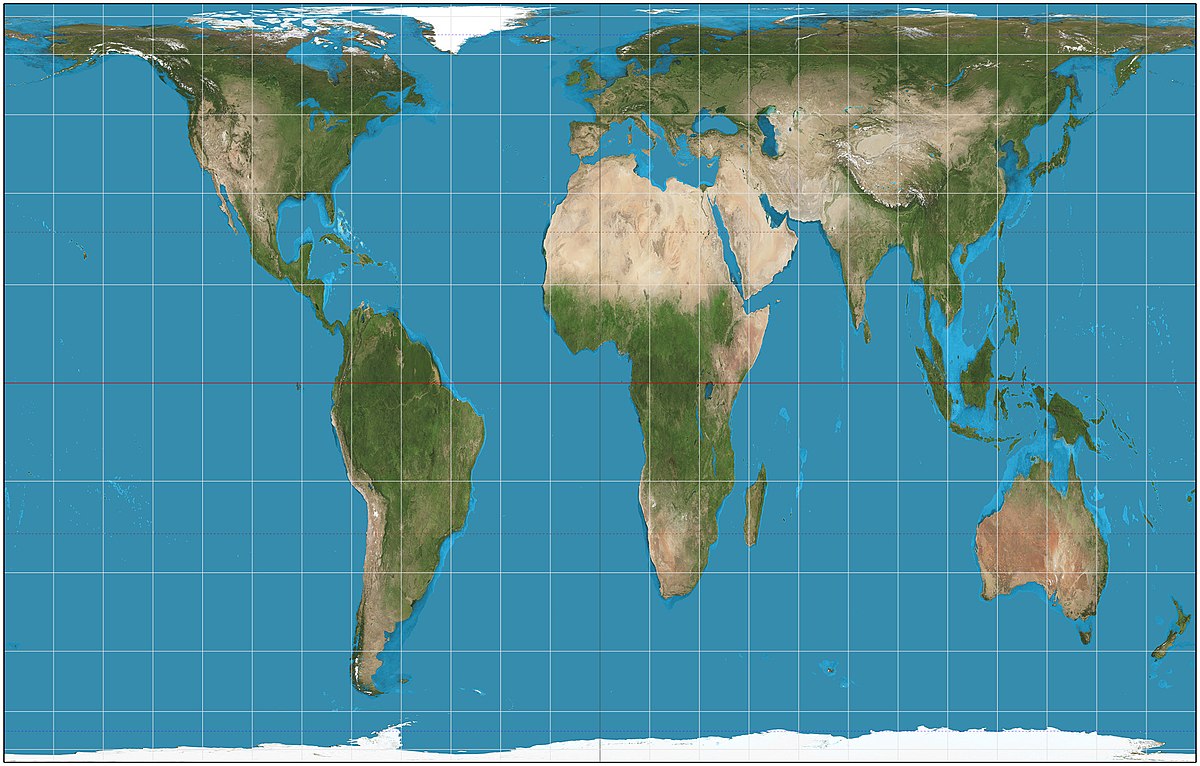
Compression
Areas can be "inflated" or "deflated" some, but not all projections.
- This can cause serious issues when you are trying to calculate statistics dependent upon area!
- Population density is a good example
- You will get hands on experience with this issue in Lab

Types of Projections
All map projections must induce distortions in order to display the 3D earth in 2D. But there are different types of projections that are designed to preserve some attributes.
- Conformal: Shapes and angles are preserved, i.e. they prevent shearing
- Equal-area: Areas is preserved, i.e. they prevent compression
- Equidistant: Distance is preserved
- Not "globally", only in certain regions, ie. the tangent/secant lines
- True-direction: Gives shortest route between points (great circle)
- Not "globally", only certain paths, ie. outward from the center of an azimuthal projection
- Compromise: Splits the difference for aesthetics
Conformal Projections
These projections are designed to maintain the shapes/angles across the map.
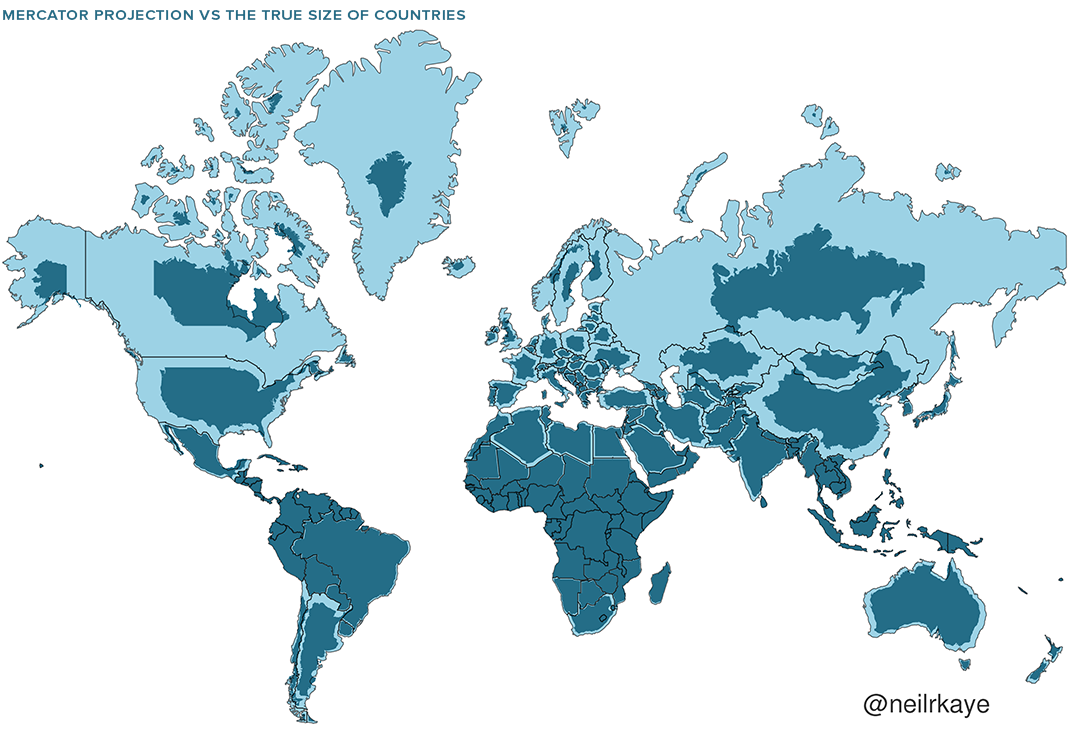
- The mercator projection is a good example
- Because it maintains shape/angles, it can be used to circumnavigate the globe in a sailboat
- But to maintain shape globally, it must severely distort area
- Scale changes across the map, poor for measuring distances or areas

Conformal Projections
These projections are designed to maintain the shapes/angles across the map.
- The lambert conformal conic projection is also a good example
- Because it is a conic projection showing a smaller region and it uses secant lines, areal distortions are less obvious/drastic
- However, the area calculations are not true to reality

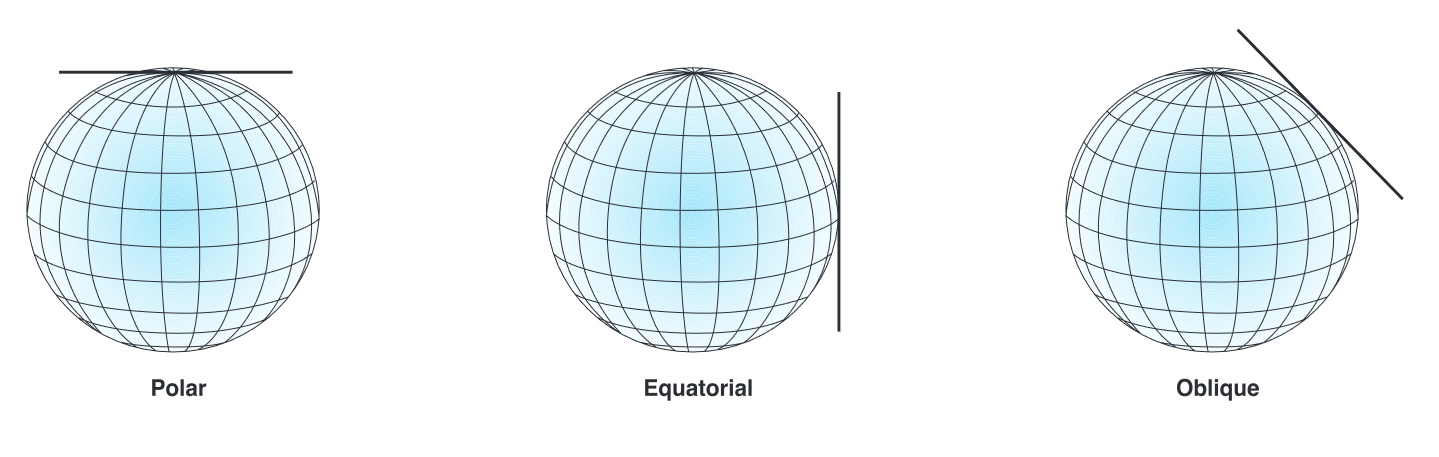
Universal Transverse Mercator (UTM)
Globe is divided into 60 strips 6° wide, spanning 80°N to 80°S.
- Minimal distortion within zones
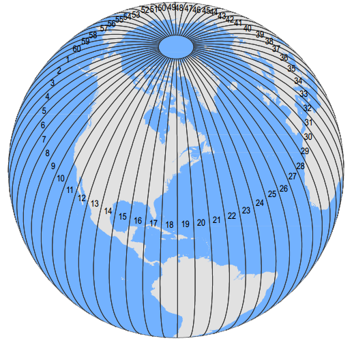
A special type of conformal projection.
- Only used for "small" areas
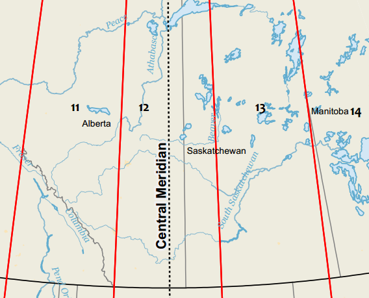
UTM Zones
Vancouver is in UTM Zone 10N.
The Mackenzie Delta, UTM Zone 8N.

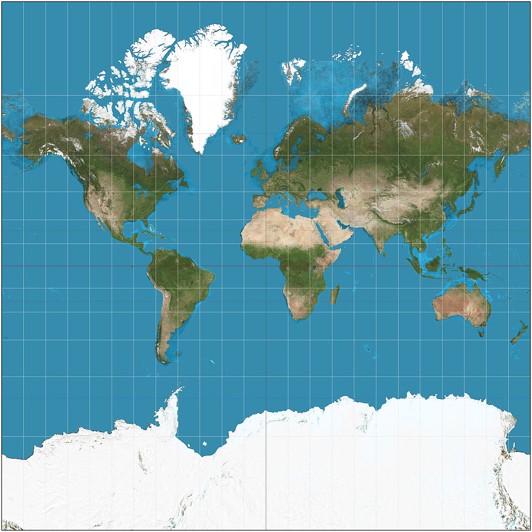
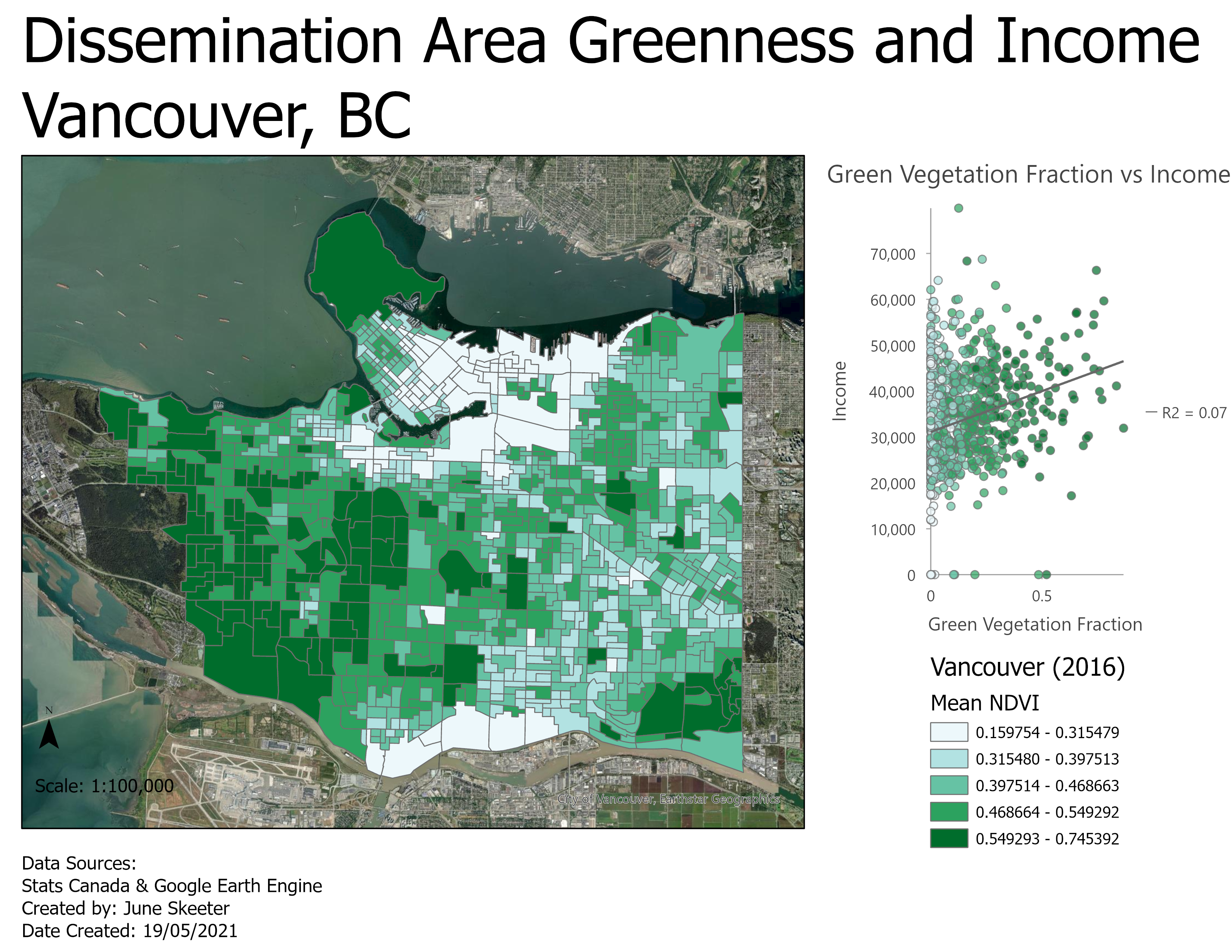
Equal Area Projections
These projections are designed to preserves area.
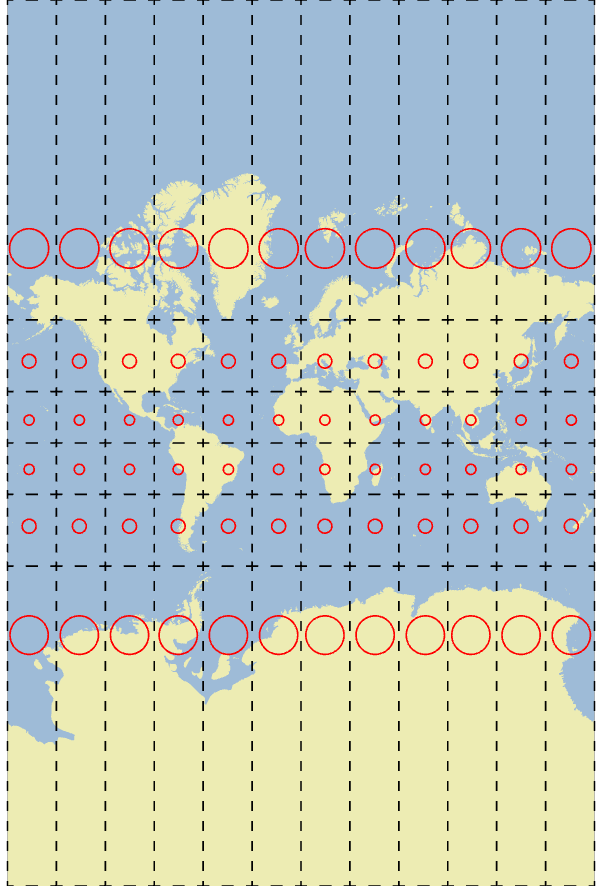
- The gall peters projection is a good example
- Because it maintains area, it can be used to calculate population density
- Very useful in GIS where area must be preserved for land analysis
- Angles/shapes are deformed so it "looks" weird
Equal Area Projections
These projections are designed to preserves area.
- The albers equal area projection is also a good example
- Because it is a conic projection showing a smaller region and it uses secant lines, shape/angle distortions are less obvious/drastic
- You can still see it, especially in the north

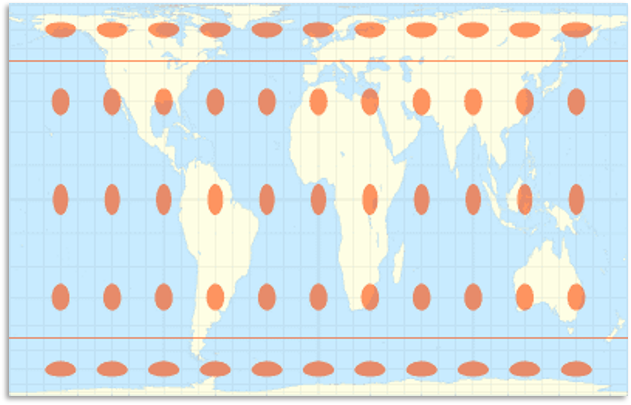
Equidistant Projections
These projections are designed to preserves distance.
- Distance cannot be preserved globally, only specific locations
- e.g. lines radiating from center of an azimuthal projection
- e.g. lines of longitude + central meridian of sinusoidal projection
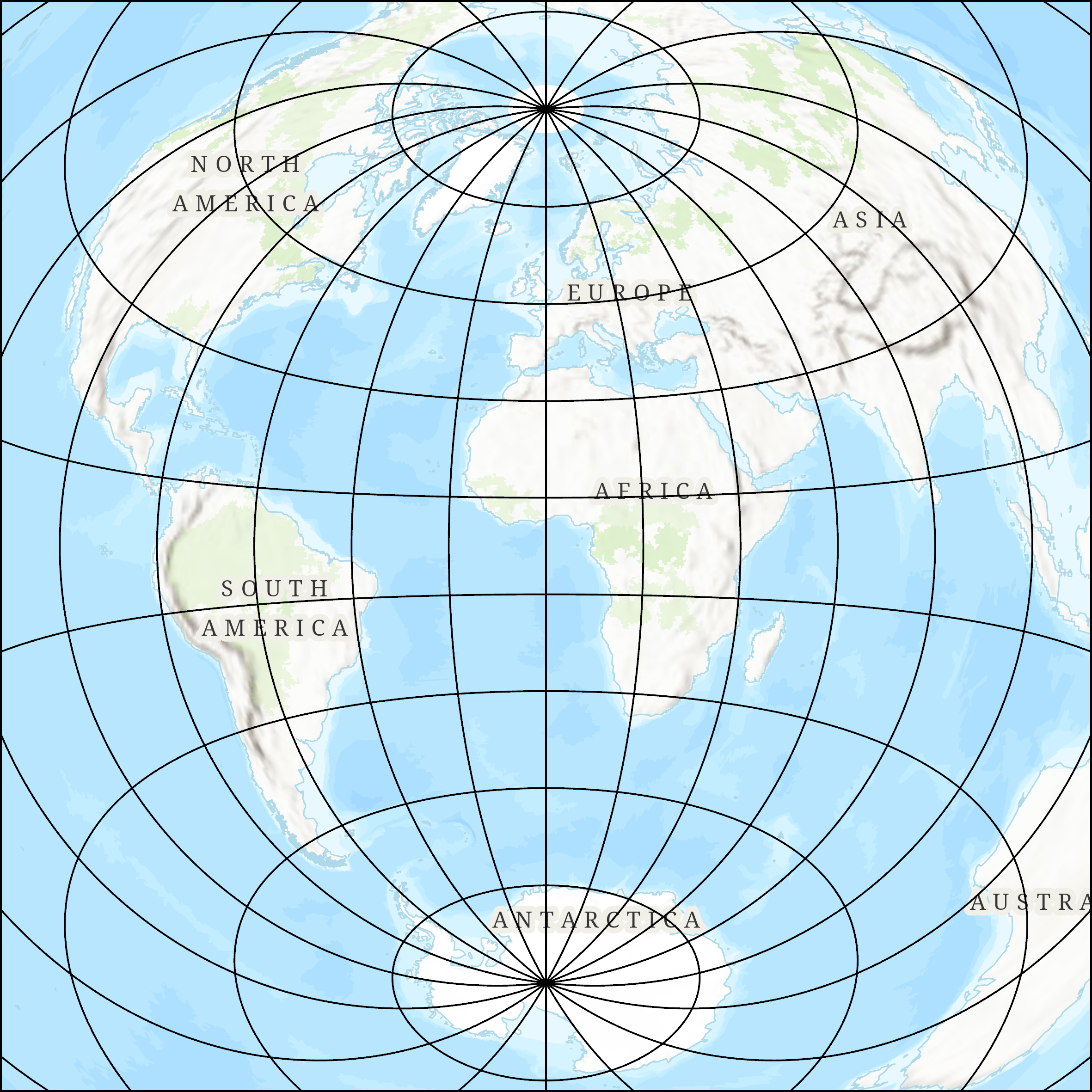


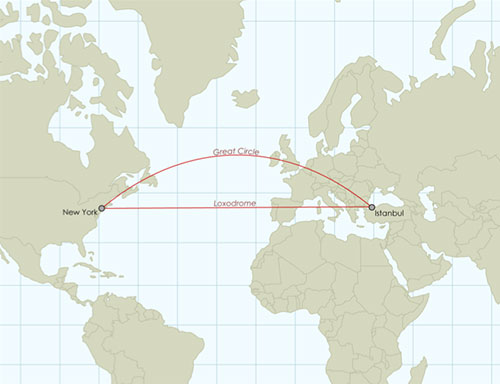
True-direction Projections
These projections are designed to preserves direction.
- Direction cannot be preserved globally, only specific locations
- e.g. lines radiating from center of an azimuthal projection
- Often, equidistant are also true direction but not always
- Will give us a "great circle" route, the shortest distance between two locations

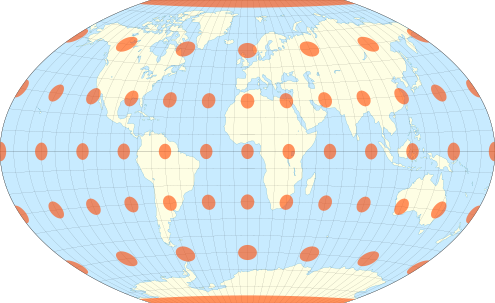
Compromise Projections
These projections are designed for aesthetics.
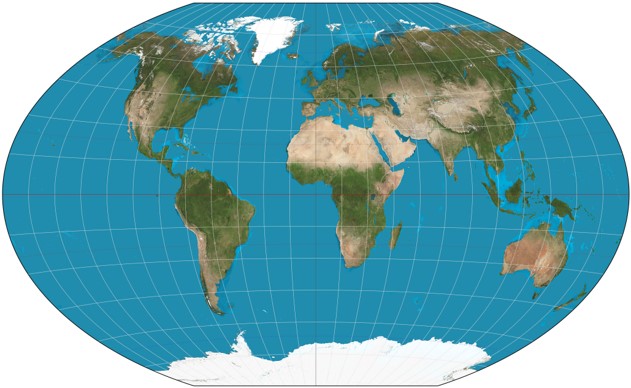
Minimize distortion without preserving any one property.
TopHat Question 3
A conformal projection will maintain which properties? (select all that apply)
- Area
- Shape
- Distance
- Angles
- Direction
- All of the above
- None of the above
What projection is right for my map?
There isn't a "correct" answer here, but there are definitely wrong answers.
- You can typically get similar results with a handful of different projections, depending on your application
- Best practice is to always use an equal area projection to calculate areas/densities
- But there are many different equal area projections
Things to Think About
Where do the data come from?
- Some organizations use a standard projection
- Stats Canada: Lambert Conformal Conic
- British Columbia: BC Environment Albers
What is the map's purpose?
- Conformal/compromise are aesthetically pleasing.
- Navigational maps, use conformal, equidistant, etc.
- Thematic maps (areas/densities) use equal area.
Map Scale
The relationship between distance on a map to distance in the real world.
- How much smaller is a unit on the map than a unit on the earth?
- i.e. 1 cm on the map = 1 km on the Earth
- Can be described:
- Graphically
- Verbally
- Representative fraction

Map Scale
Small Scale Zoomed out, large area, more generalization, less detail.
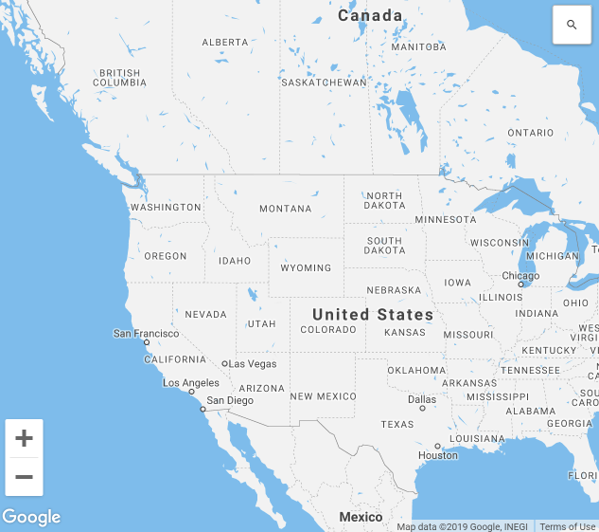
Large Scale Zoomed in, small area, more detail, less generalization.
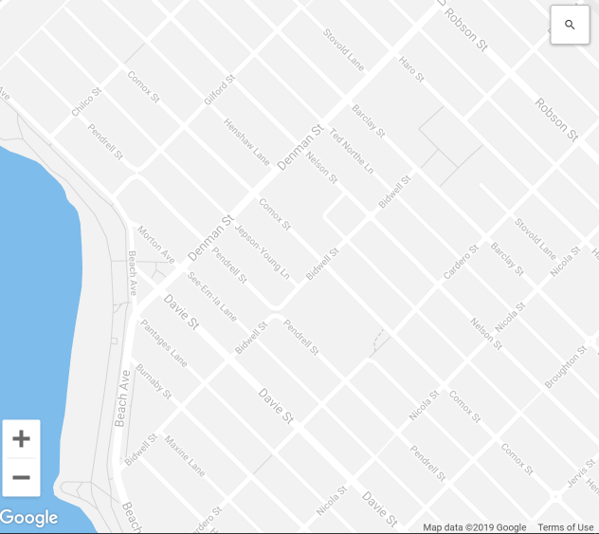
Map Scale
Small Scale 1:10,000,000
1/10,000,000 = 0.0000001

Large Scale 1:1,000
1/1,000 = 0.001

Map Scale
All maps require simplification of real world features. The degree of simplification is a function of the map's scale.
- Smaller scale maps require more generalization.
- Larger scale maps can include more detail.
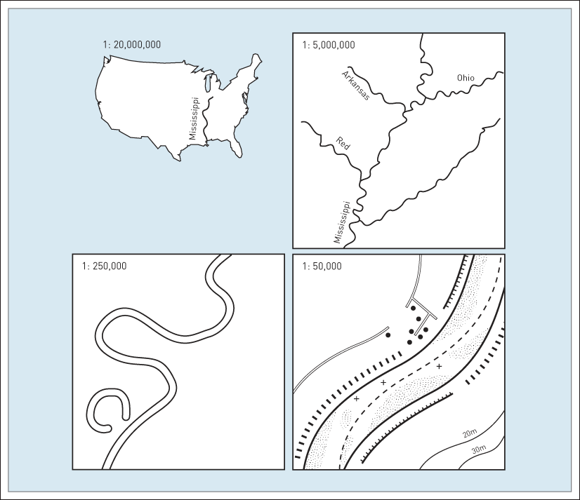
Map Scale & Projection
Map scale will impact our choice of projection.
- Projections that work at 1:000 aren't necessarily suited for a 1:10,000,000 map
- With conformal projections like the Mercator, scale changes with position on the map
- Preserves scale "locally"
- Scale is grossly distorted globally
TopHat Question 4
A large scale map shows a _____ area of the earth and small scale map shows a _____ area of the earth.
TopHat Question 5
On a scale of 1 to 5: How do you feel about the lecture topics covered in Module 2 (Steps of Abstraction & Map Projections)?
1 = It makes no sense at all.
3 = Unsure.
5 = I makes perfect sense.
(Participation points only, please answer honestly)
TopHat Question 6
Are there any topics from Module 1 or Module 2 which you would like me to discuss further before moving on to Module 3?
- If not, just say No
- If yes, please keep your response short. List a few concepts you find particularly confusing, separated by a comma
- e.g. "Datums, tangents vs. secants"
(Participation points only, please answer honestly)