Classifying Data
Descriptive Statistics
| Statistic | Nominal | Ordinal | Interval | Ratio |
| Equality | x | x | x | x |
| Counts/Mode | x | x | x | x |
| Rank/Order | x | x | x | |
| Median | ~ | x | x | |
| Add/Subtract | x | x | ||
| Mean | x | x | ||
| Multiply/Divide | x |
Measures of Central Tendency
Highlight the "central" feature in a dataset.
- Mode: The most frequent value in a set
- Median: The middle value in a set
- Data is ranked to find the center point
- 50% above, 50% below
- Not impacted by outliers
- Mean: The sum of all values divided by the number of values
- Impacted by outliers
Measures of Dispersion
These statistics give context a measure of central tendency.
- Range: The difference between the maximum and minimum values
- Inter-quartile Range: Difference between 75th and 25th percentile value
- Spread around the median (50th percentile), not influenced by outliers
- Standard Deviation: $\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^n (x_i - U)^2}$
- Spread of data values (x) around the mean(U), influenced by outliers
Frequency Distribution
Frequency of occurrence in a qualitative data.
- Counts per category
- Bar charts are a useful tool for visualizing frequency distributions
Probability Distribution
Probability of occurrence in a quantitative dataset.
- Normal Distribution: idealized, based on distance from the mean in standard deviations.
- Assumed distribution in many statistical tests.
| ±1 $\sigma$ | 68% of observations |
| ±2 $\sigma$ | 95% of observations |
| ±3 $\sigma$ | 99.7% of observations |
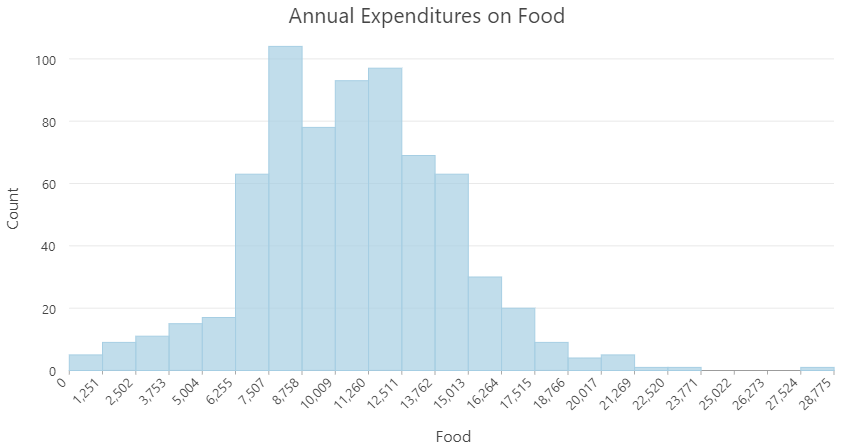
Histograms
Useful for quantitative data.
- Orders data and groups data into bins of consistent width
- Helpful for:
- Approximating probability distribution
- Grouping data into classes
- Outlier detection
- Similar to bar charts, but not the same thing!
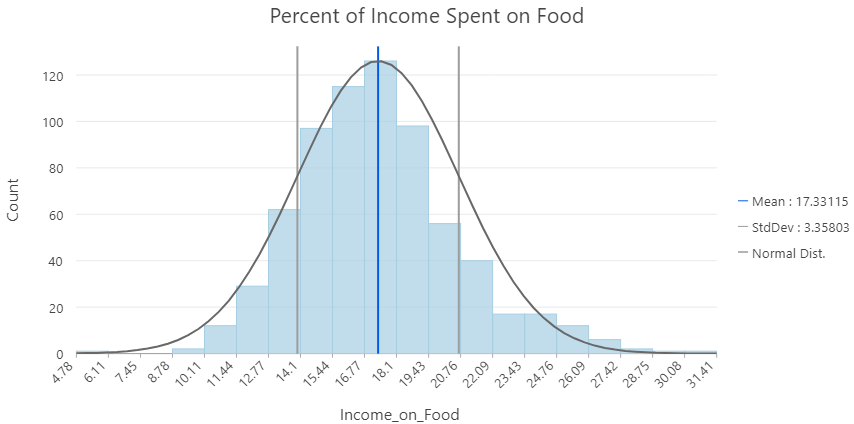
Deviating from the Norm
Data rarely fits a normal distribution perfectly:
- Skew: deviates from a normal distribution
- Tails with outliers
- Kurtosis: deviates from a normal distribution
- Dispersed or clustered
Near Normal
Skewed Normal
Highly Skewed
TopHat Question 1
If you are working with nominal or ordinal data, and you want see how many observations you have for each category, you would use:
- A histogram to plot a probability distribution
- A histogram to plot a frequency distribution
- A bar chart to plot a probability distribution
- A bar chart to plot a frequency distribution
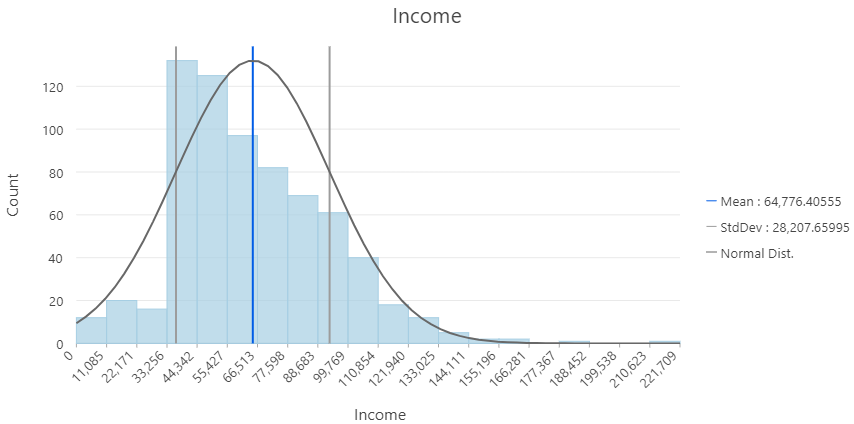
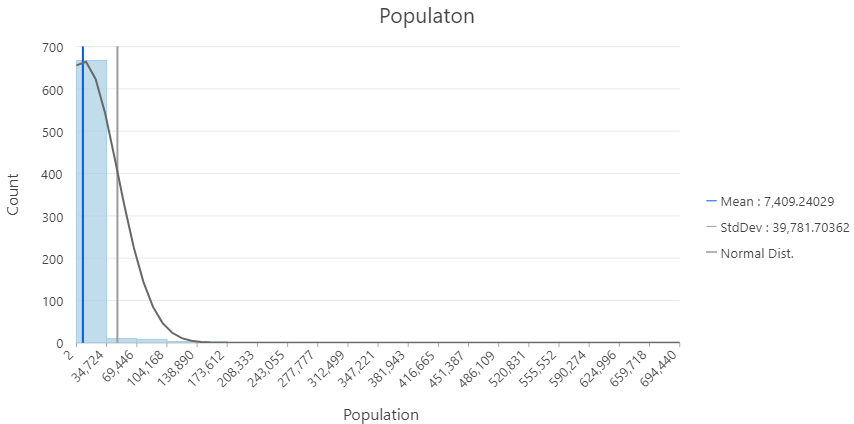
Normalizing Data
Allows us to account for confounding variables that mask or hide patterns in our data.
- Helpful to scale or normalize a value by a another value - time, area, population etc.
- Examples:
- Income vs. money spent on food
- Population vs. shape area
Highly Correlated
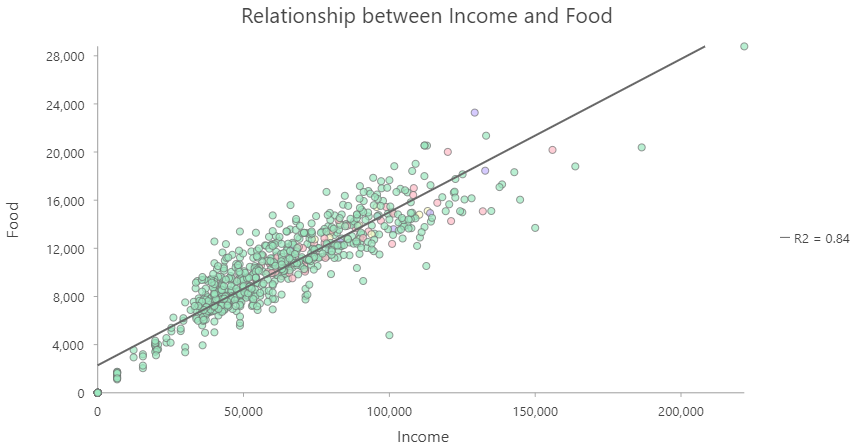
No Correlation
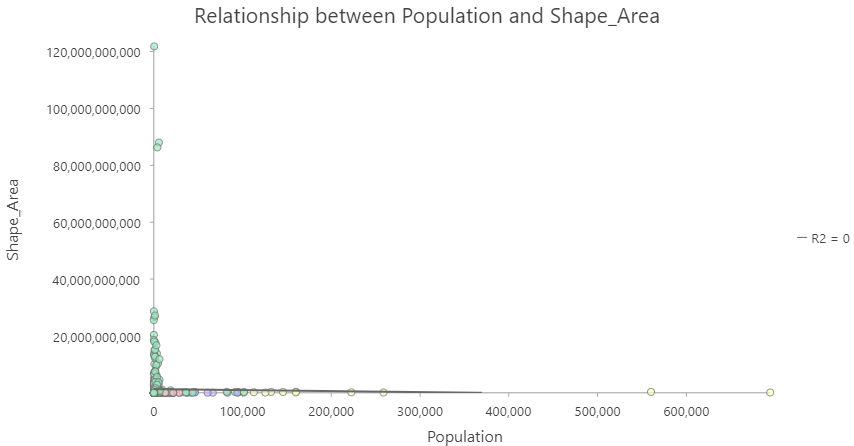
Multiple Confounders
It isn't always straightforward to account for multiple variables.
- ex: COVID rates by age groups

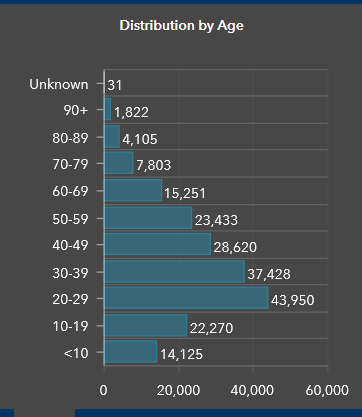
- Population by age group
- Workforce participation
- Occupational exposure
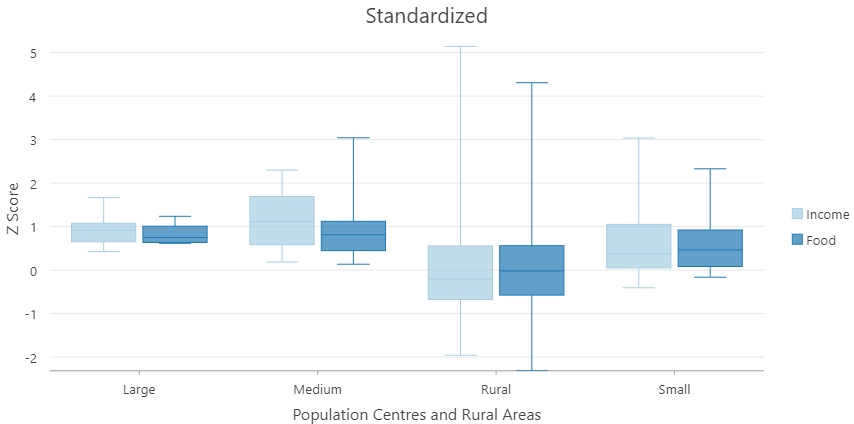
Standardizing
Also allow us to compare between two or more variables in different units / scales.
- $z = \frac{x-\overline{U}}{\sigma}$
- Similar idea to normalizing, but:
- Removing the mean and standard deviation from multiple variables
TopHat Question 2
Which of these countries has the highest population density? * Populations and Areas are approximate, given to two significant figures for convenience.
- Monaco: Pop (37,000), Area (2 km2)
- Singapore: Pop (5,500,000), Area (720 km2)
- China: Pop (1,400,000,000), Area (9,600,000 km2)
Classification Methods
Unsupervised:
- Data defined classes - the user decides on the number of classes
- The rest is left of up to an algorithm
Supervised:
- User defined - the user explicitly defines classes
- Or provides set of classes as training data
- Degree of user input is variable, more than unsupervised
Common Examples in Arc Pro
Vancouver dissemination area populations
- Not classified
- Color scheme is stretched between min/max
- Difficult to see patterns
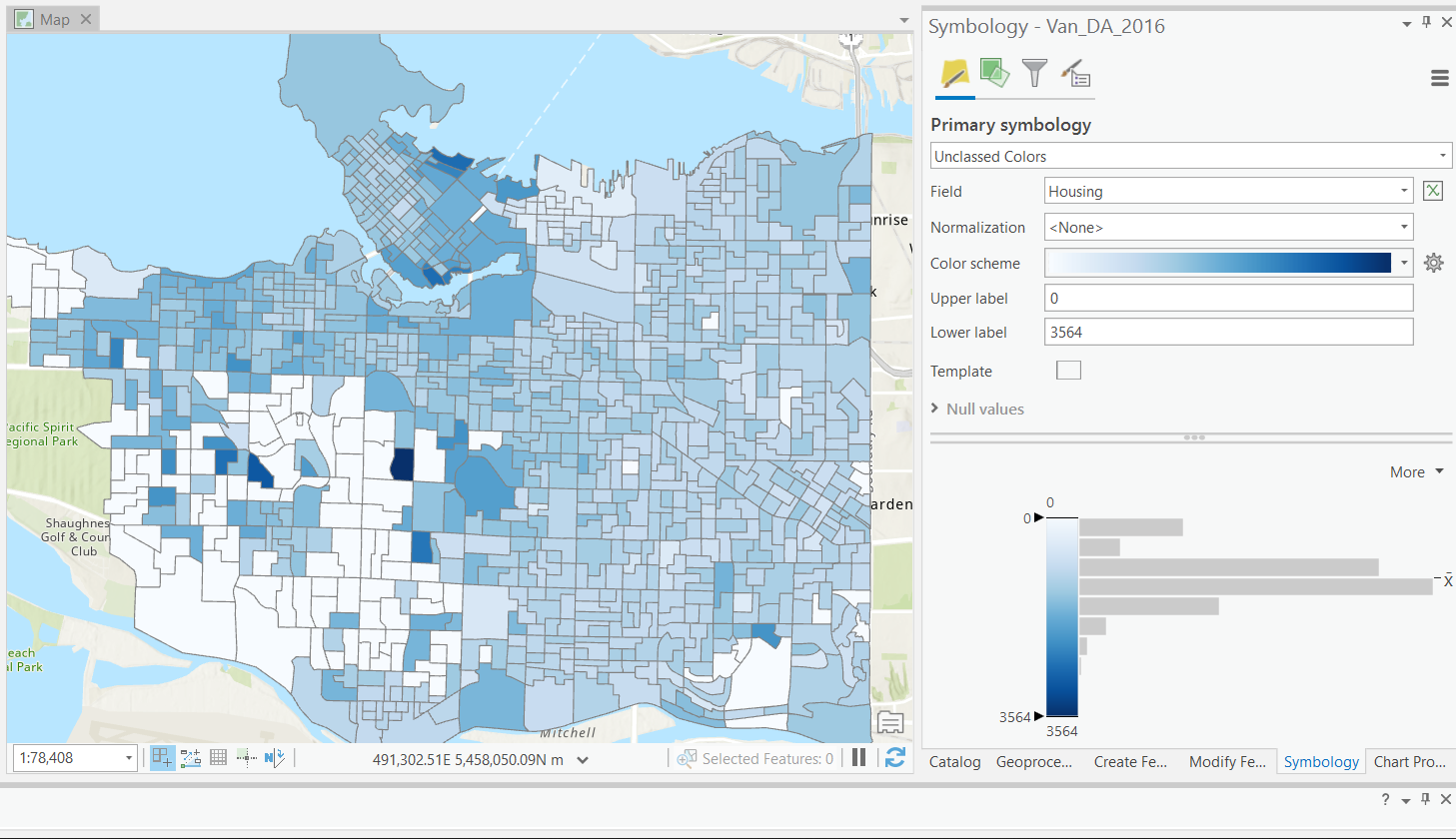
Equal Interval
One of the simplest classification schemes.
- Data is split to classes of equal width based on the range.
- Unsupervised: user defines number of bins.
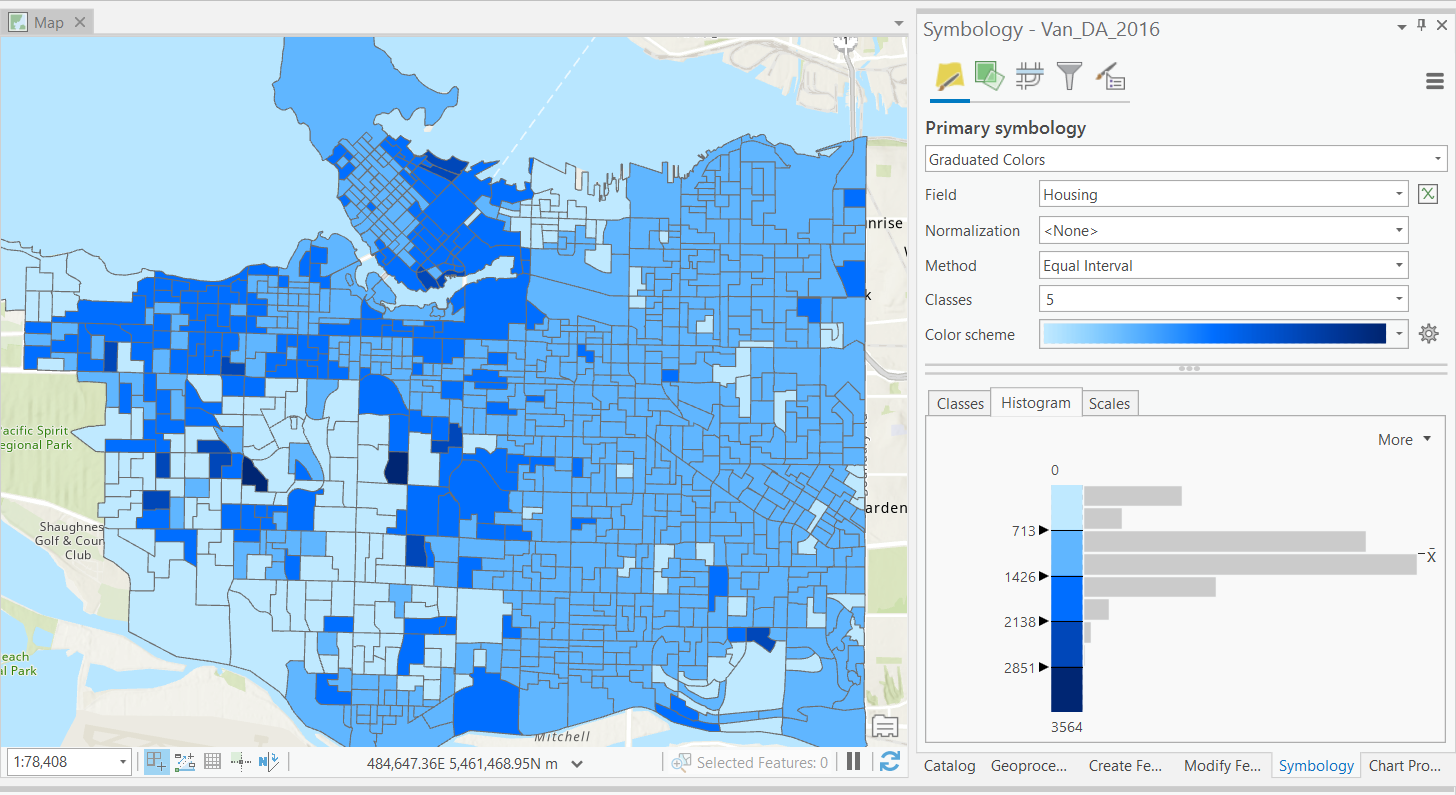
Defined Interval
Another of the simplest classification schemes.
- Data is split to classes of equal width based on the range.
- Unsupervised: user defines bin width.
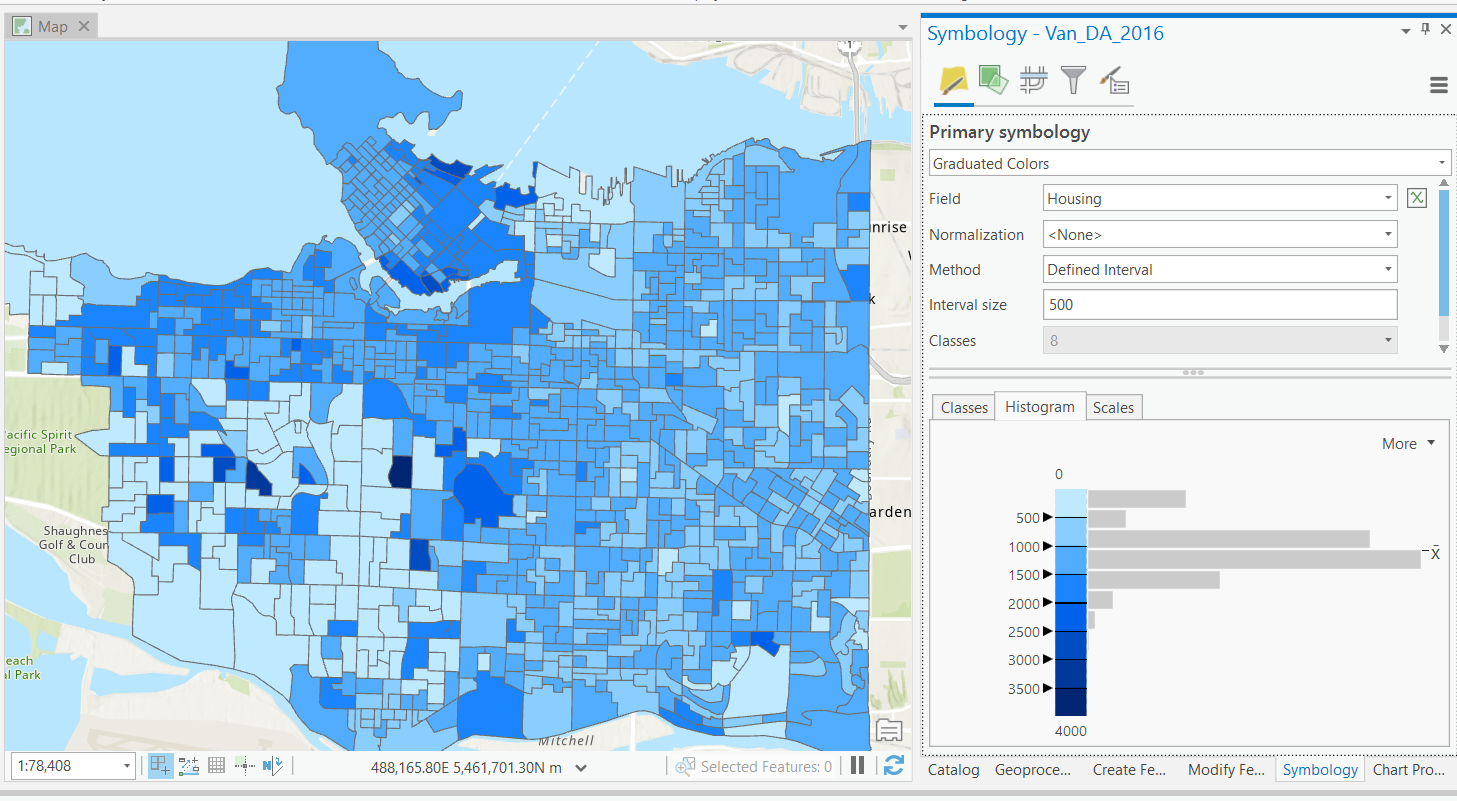
Quantiles
Slightly more complex classification scheme.
- Data is split into classes by percentiles.
- e.g. 0-20%, 20-40%, ... 80-100%.
- Unsupervised: user defines number of bins.
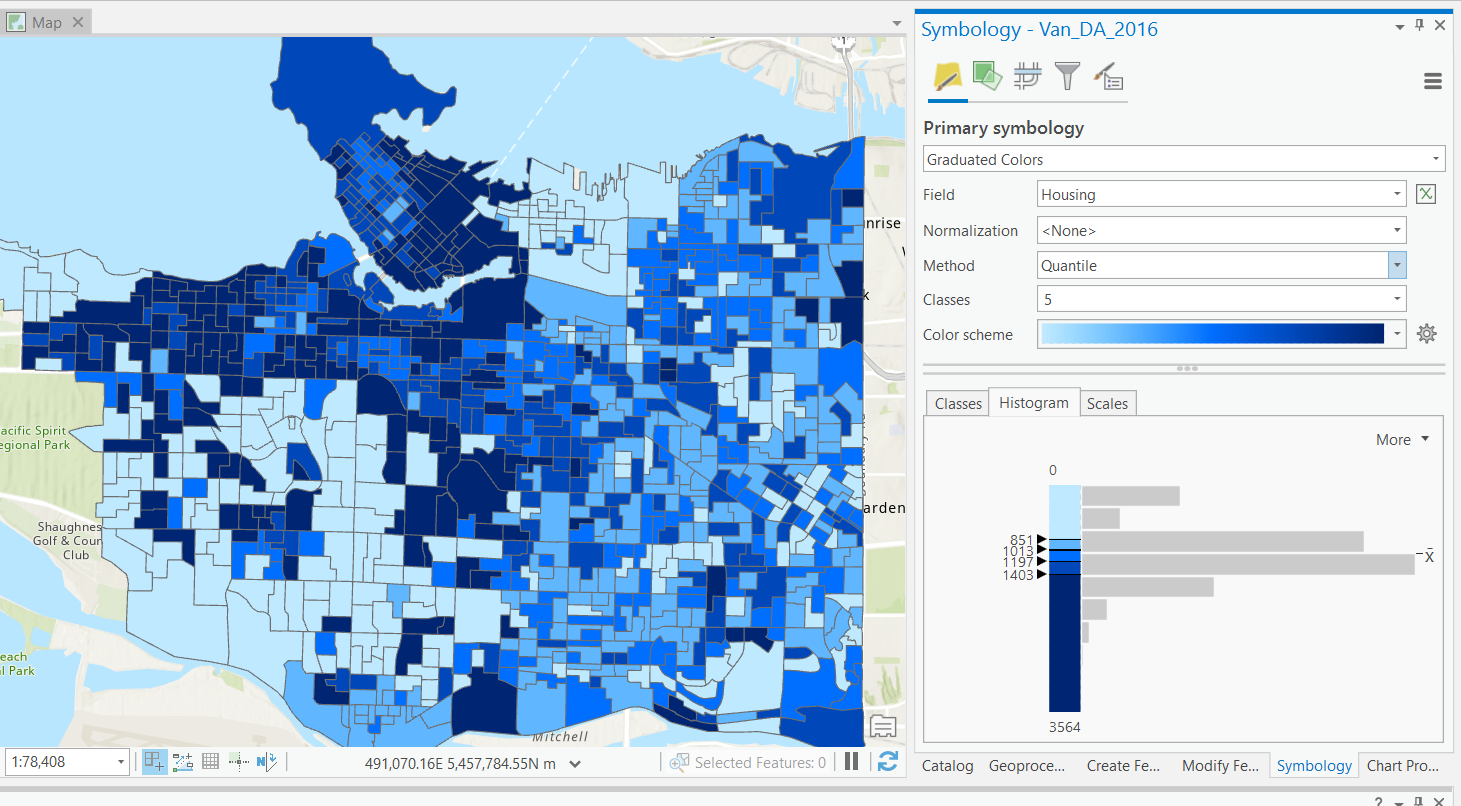
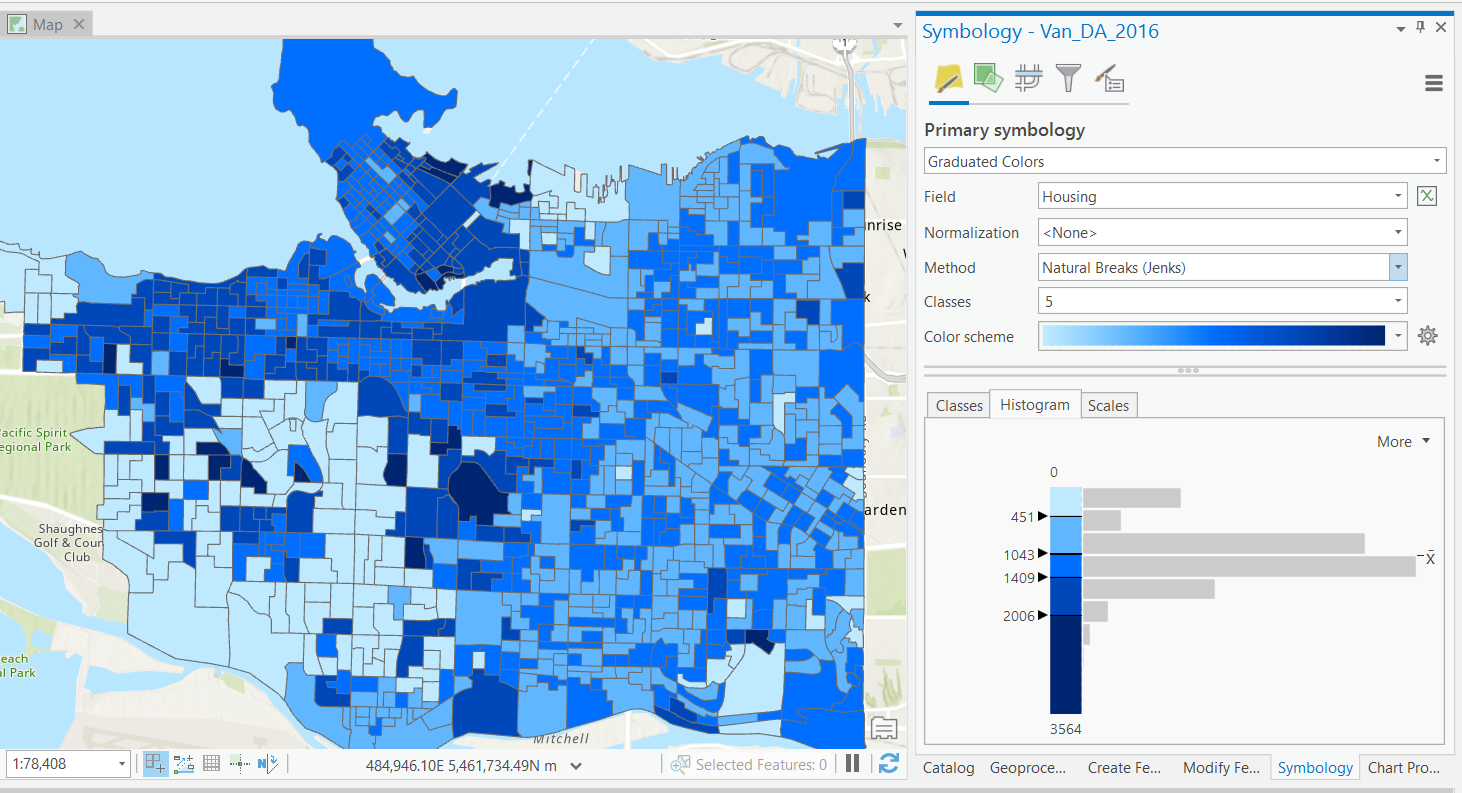
Natural Breaks
More complex, data is split using the Jenks algorithm.
- Optimizes splits, by maximizing within group similarity and between group dissimilarity.
- "Natural" classes.
- Unsupervised: user defines number of bins.
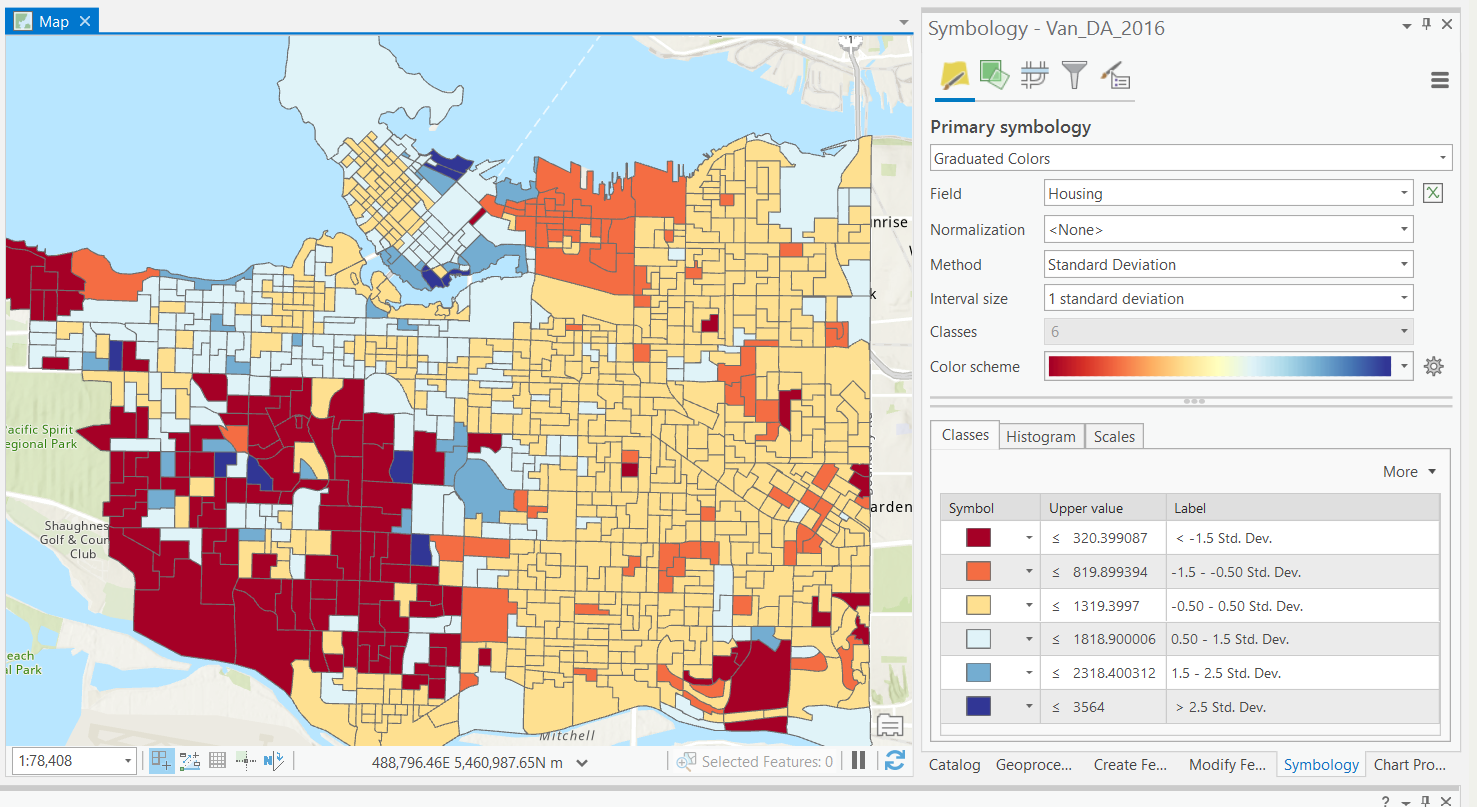
Standard Deviation
Informative to "experts", but not accessible for all.
- Classes based on "distance" from the mean in standard deviations.
- Unit-less, converts to interval data.
- Diverging color maps.
- Unsupervised: user defines number of bins.
Manual Breaks
Supervised: User defines break values.
- Allows us to choose more meaningful break values if necessary.
- Incorporate multiple factors
- Influence the way the data is perceived.

TopHat Question 3
This classification method seeks to maximize the similarity between data values within groups and maximize the dissimilarity in data values between groups. It tries to find the "optimal" splits within a dataset.
- Manual Breaks
- Quantiles
- Natural Breaks
- Equal Interval
- Standard Deviation
More Complex Methods
There are many classification methods that are a bit too complex to actually perform in this course.
- I'm introducing some because important to be aware of them.
- You'll encounter them if you continue with GIS.
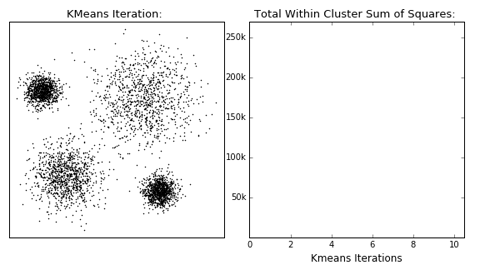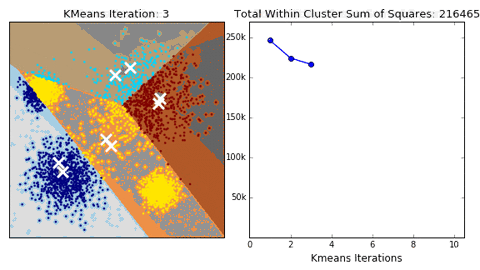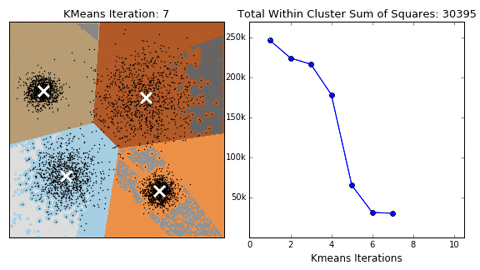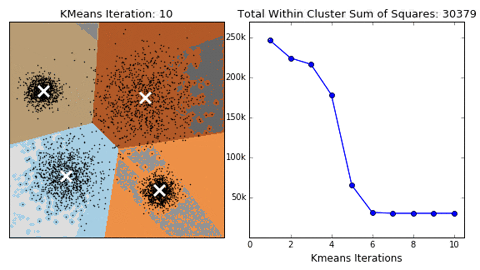
K-means
Algorithm uses random steps to group data into clusters.
- Unsupervised: user defines number of bins & iterations.
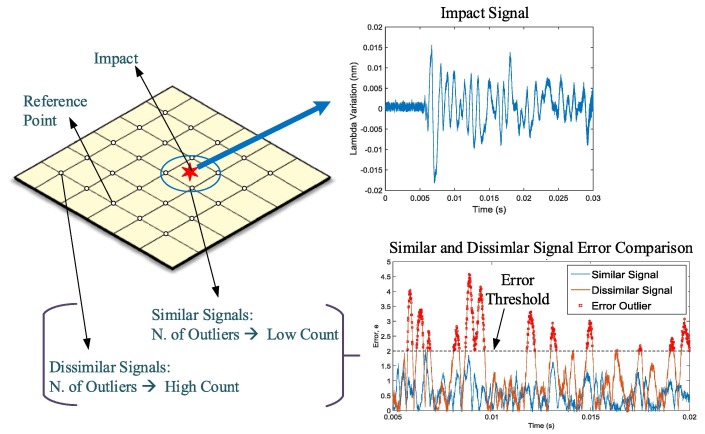
Median Absolute Deviation
Used for automated detection of outliers.
- Unsupervised: user defines error threshold.
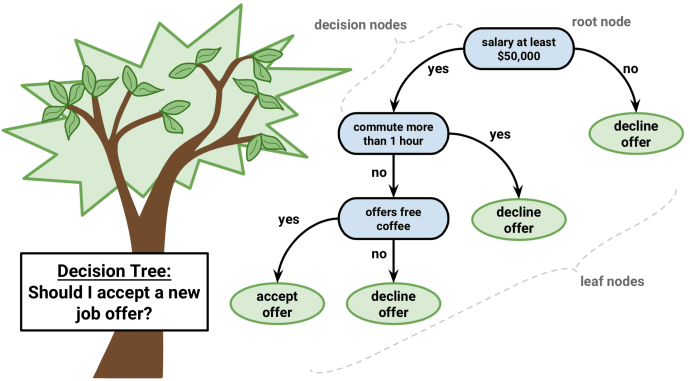
Decision Trees
Fit training data to user defined categories.
- Supervised: user provides training classes.
- Automated: algorithm determines break values.
- Risk of over-fitting
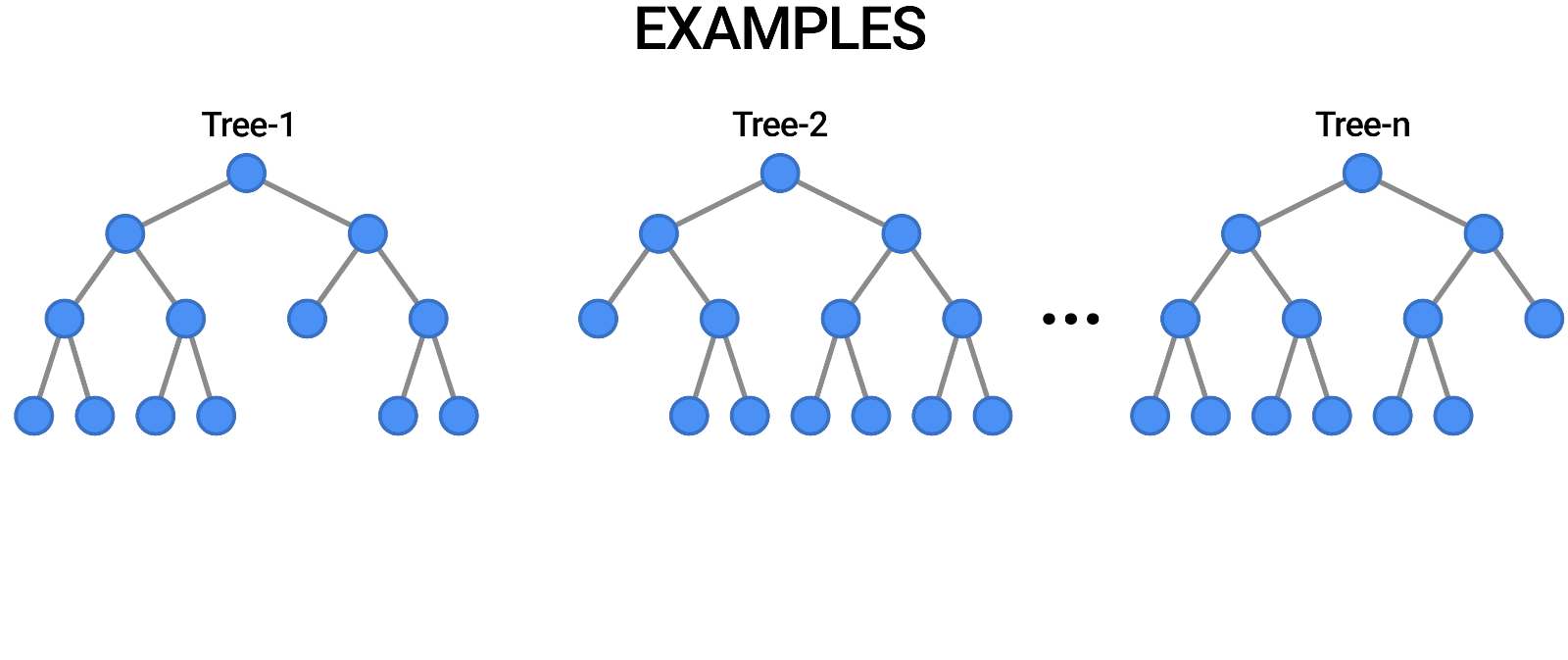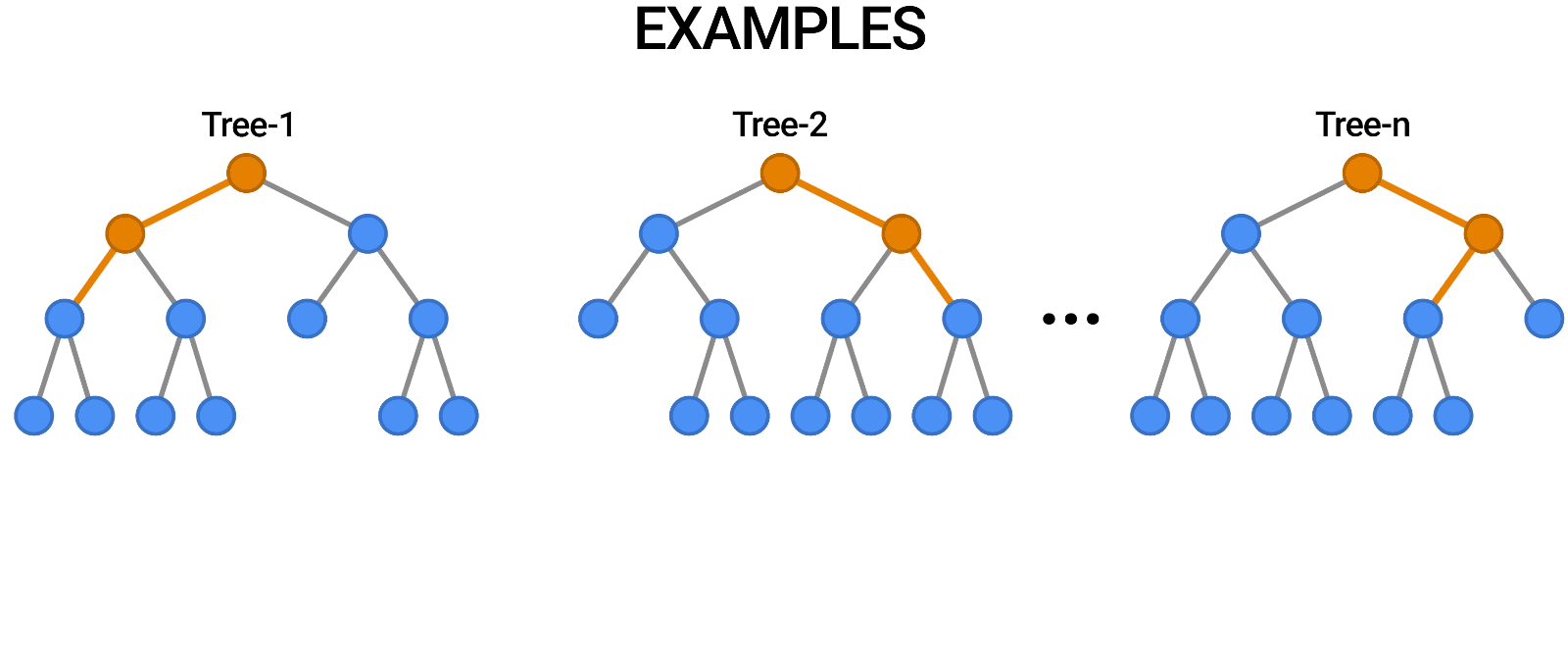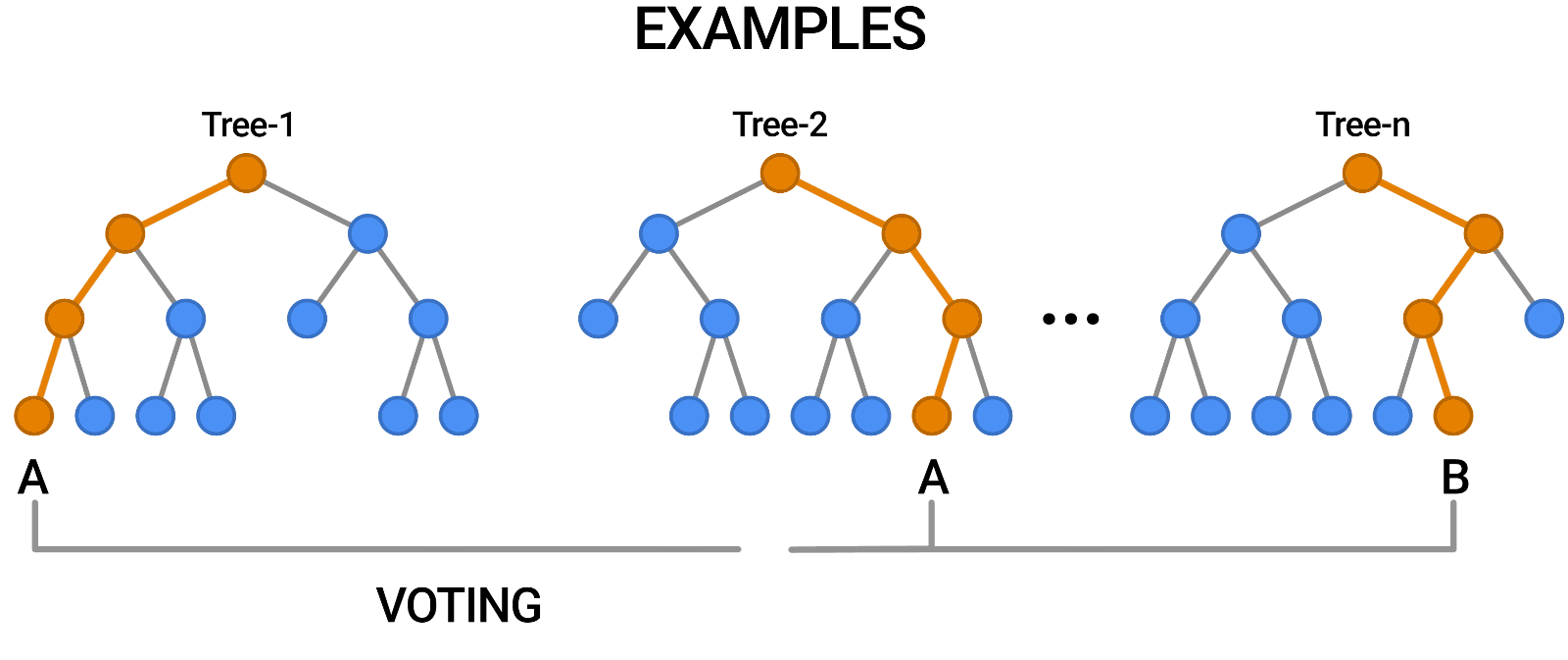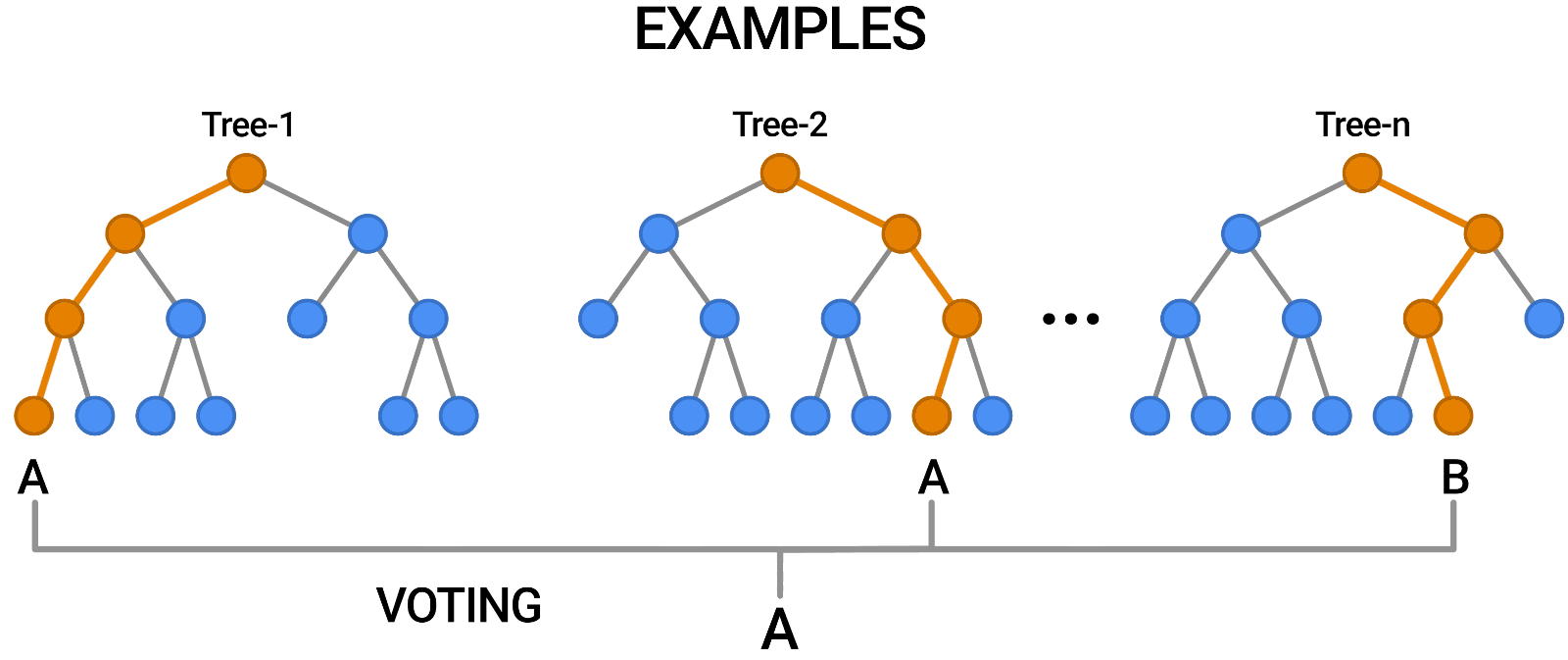
Random Forests
Multiple trees (>100) can be averaged to increase performance and generalization.
- Supervised: user provides training classes and "hyperparameters".
- Automated: algorithm determines break values.
- Low risk of over-fitting
Landscape Classification
Multiple trees (>100) can be averaged to increase performance and generalization.
- Supervised: user provides training classes and "hyperparameters".
- Automated: algorithm determines break values.
- Low risk of over-fitting
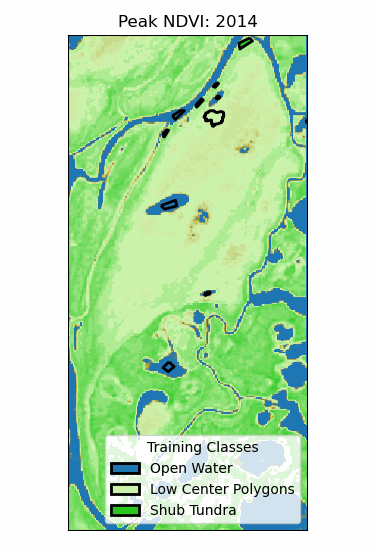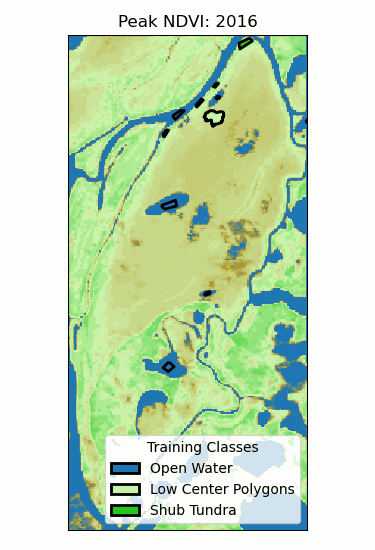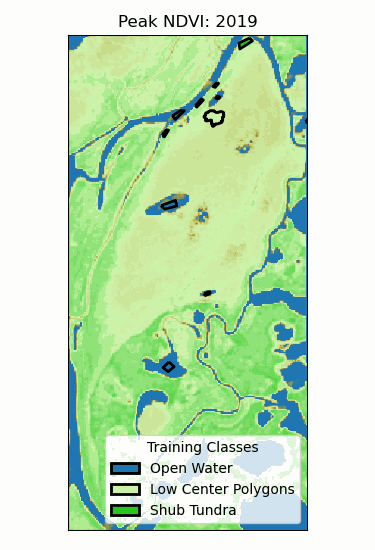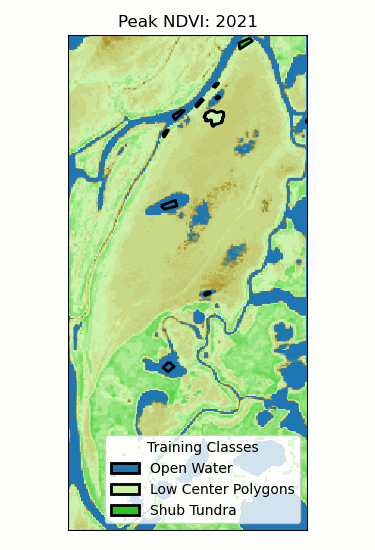
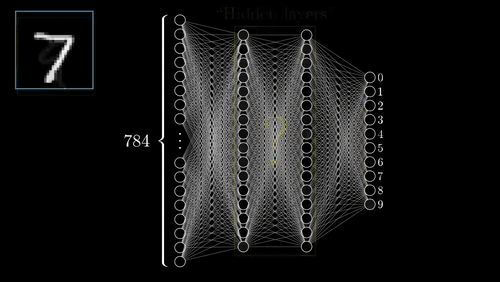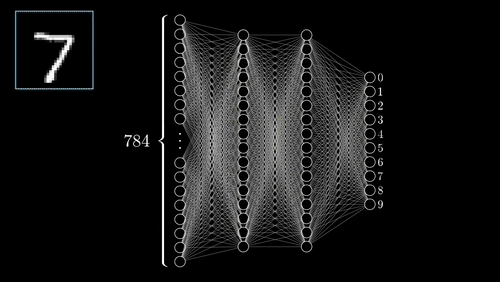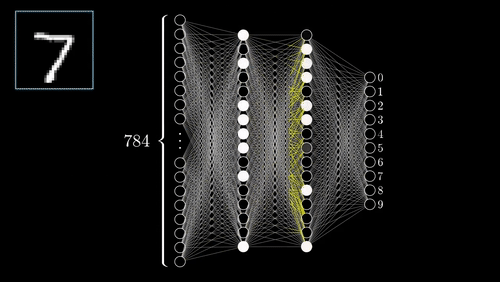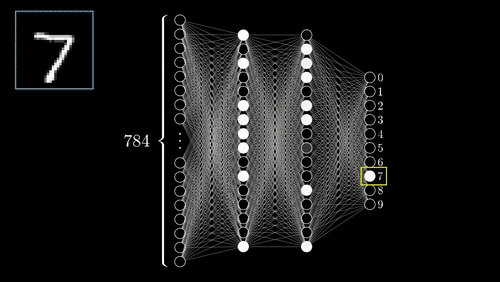
Neural Networks
One of the most complex methods.
- Supervised: user provides training classes and "hyperparameters".
- Automated: algorithm maps relationships in dataset.
- Risk of over-fitting
- Requires careful inspection
TopHat Question 4
Unsupervised classification methods typically require more user input than supervised classification methods.
- True
- False